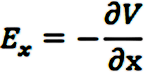PROBLEMAS DE ELECTROSTATICA: POTENCIAL
Ley de Coulomb. Campo eléctrico.
En estos problemas vamos a trabajar con:
-
El trabajo de las
fuerzas eléctricas.
-
Diferencias de
potencial eléctrico. en distintas distribuciones de cargas.
-
Materiales
c o n d u c t o r e s.
- Elctrostática de los capacitores.
PROBLEMA 2.1.–
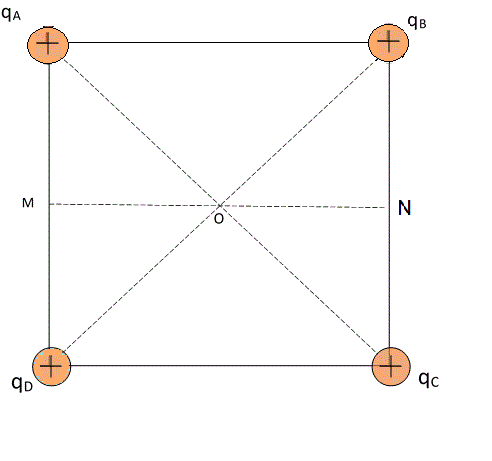
En los vértices del cuadrado ABCD hay cargas puntuales: qA = qB = qC = qD = 2 nC. El lado del cuadrado es L=20 cm.
En el punto M, punto medio del lado AB, hay un electrón que inicialmente está en reposo. Debido a la atraccion las cargas que lo rodean, el electrón comienza a moverse. (el peso del electrón es despeciable y en el recinto se ha practicado el vacío).
Calcular:
a) La aceleración inicial del electrón
b) Su velocidad cuando pasa por el punto O, centro del cuadrado.
c) Su velocidad cuando llega al punto N, punto medio de lado CD.
Carga del electrón qe = -1,6 . 10-19C
Masa del electrón me = 9,1 . 10-31Kg
|
 |
R: a) aM = 1,1323 . 1014 m/s2 b) VO = 2,044 . 106 m/s. c) VN = 0
PROBLEMA 2.1.bis–
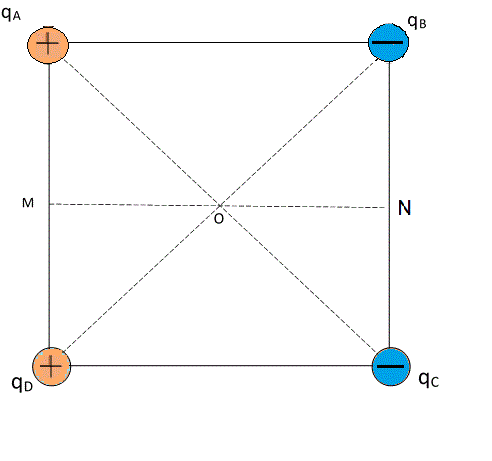
En los vértices del cuadrado ABCD hay cargas puntuales: qA = qD = 2 nC qB = qC = -2 nC. El lado del cuadrado es L=20 cm.
En el punto M, punto medio del lado AB, hay un ión positivo que inicialmente está en reposo. Debido a la atracción las cargas que lo rodean, el ión comienza a moverse. (el peso del ión es despeciable y en el recinto se ha practicado el vacío).
Calcular:
a) La velocidad vO del ión cuando pasa por el punto O, centro del cuadrado.
b) La velocidad vN del ión cuando pasa por N, punto medio de lado CD.
c) Para pensar: ¿ Cuánto vale la relación
vN /vO ? ¿ Porqué ?
Carga el ión qi = -1,6 . 10-19 C
Masa del ión mi = 5 . 10-25 Kg
|
 |
| |
R: a) vO = 11285,5 m/s b) vN 15.960 m/s c) Por simetría VOM y VON son ...
PROBLEMA 2.2.–
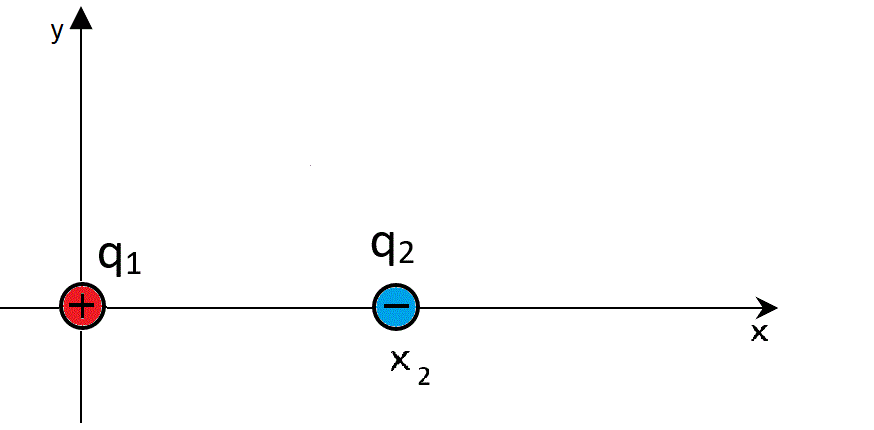
En el eje x hay dos cargas puntuales de distinto signo:
q1 = 40 nC y q2 = -10 nC.
La carga q1 está el origen de coordenadas y la carga q2 tiene abscisa x2 = 15 cm.
a) Hallar las coordenadas de el o los puntos del eje x en los cuales se anula el potencial eléctrico con respecto al infinito.
b) Calcular el campo eléctrico en esos puntos.
c) Para pensar: Analizar la variación del potencial a lo largo del eje x ¿Dónde es creciente y donde decreciente? ¿Tiene algún máximo relativo? si-no ¿Porqué? En el caso afirmativo: ¿Cuánto vale Ex en ese punto? ¿Porqué? |
 |
R: a) x = 12 cm y x = 20 cm b) 125.000 N/C y 27.000 N/C respectivamente c) Tener en cuenta que es cero en x = 20 cm y en infinito d) Tener en cuenta que δ V / δ x = Ex
PROBLEMA 2.3.–
|
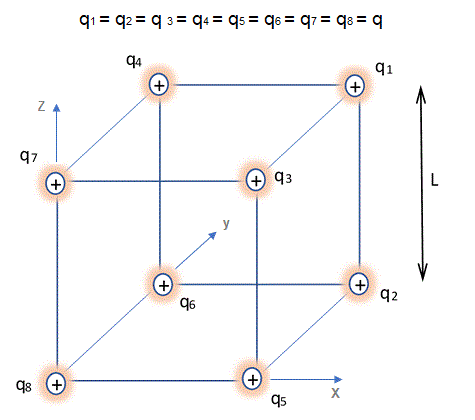
En cada uno de los vértices de un cubo de lado L hay cargas puntuales q. Expresar en función de L y q :
a) El potencial eléctrico en el centro del cubo con respecto al infinito.
b) El potencial eléctrico en el centro de una de las caras con respecto al infinito.
c) El trabajo realizado por las fuerzas eléctricas si se la lleva una de las cargas hasta el infinito.
d) El trabajo realizado por las fuerzas eléctricas si se la lleva una de las cargas hasta el centro del cubo
|
 |
R:
a) Vo = 16/3.√3 K.q/L b) (4 √2 + 4/3 √6) K.q/L c) W = (3 + 3/2 √2 +1/3 √3 ) K. q2 / L
PROBLEMA 2.4.–
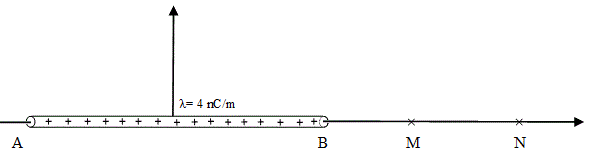
Una varilla delgada tiene una carga eléctrica uniforme λ = 4 nC/m a lo largo de toda su longitud. La varilla tiene 12 cm de largo. El punto M se encuentra sobre el eje de la varilla a 18 cm a la derecha de su punto medio. El punto N se encuentra sobre el eje de la varilla a una distancia de 24 cm a la derecha del punto medio. Si en el punto M se coloca un ión positivo, inicialmente en reposo, se pide calcular su velocidad y aceleración del cuando pasa por el punto N, teniendo en cuenta que el ión se mueve solo por la acción de las fuerzas eléctricas. Justificar las respuestas a partir de las leyes básicas de la electricidad.
Carga del ión = 6,4 10-19 C Masa del ión = 3,2 10-24Kg
|
 |
R:
VN = 1.620 m/s aN = 16.106 m/s2
PROBLEMA 2.5.–
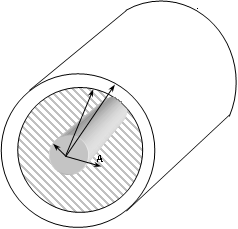
Un cable coaxial está formado por un conductor central cilíndrico de 2 mm de diámetro rodeado por un conductor cilindrico o blindaje de 6 mm de diámetro interior. Entre ambos conductores hay material aislante dieléctrico de permitividad relativa εr = 5. El conductor central está a un potencial de +40 V con respecto al conductor exterior (tierra).
Calcular:
a) El campo eléctrico en un punto A que está a: rA= 2 mm del centro.
b) La carga λ que hay en el conductor central por cada metro de longitud:λ
c) La capacidad de cable coaxial por cada metro de longitud. |
 |
R:
a) EA = 18.204,8 N/C
b) λ = 10,1 nC/m
c) C/L = 2,5 -10 f
PROBLEMA 2.6.–
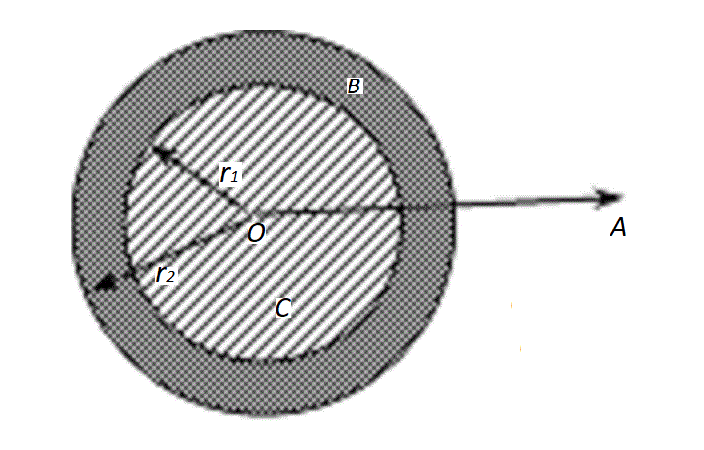
Una esfera conductora de radio r1= 4 cm estś recubierta por una capa de goma que forma una esfera hueca, de radio exterior r2= 5 cm. El punto A, estś a 9 cm del centro O. Como consecuencia de la carga de la esfera conductora en el punto A el campo eléctrico tiene dirección saliente y módulo EA = 20.000 N/C. La constante dieléctrica relativa de la goma es k = 6.
Se pide calcular:
a) El potencial del punto O, centro de la esfera con respecto al infinito.
b) El potencial del punto O, centro de la esfera con respecto al punto A.
|
|
Ver problema
1.20.- R: a) V
O-∞ = 3375 V b) V
O-A = 1575 V
PROBLEMA 2.7.–
|
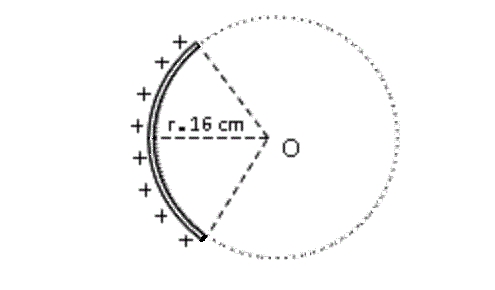
Un arco de circunferencia tiene una carga eléctrica de 80 nC uniformemente distribuida a lo largo de su longitud. Su radio es r = 16 cm. Hallar el potencial eléctrico del centro O con respecto al infinito.
|
 |
R: Potencial en O respecto del infinito = 4.500 V
PROBLEMA 2.8.–
|
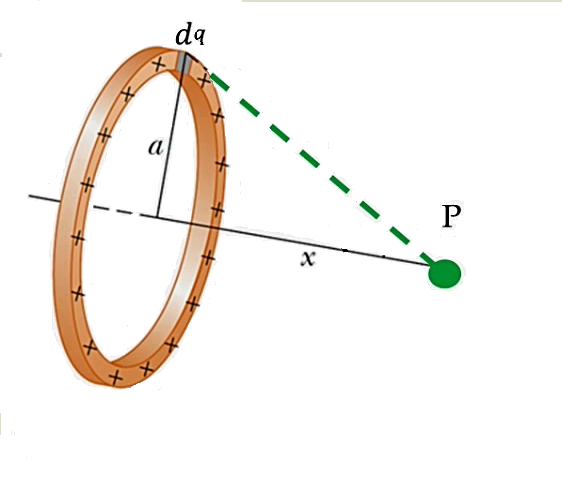
Una espira circular de alambre delgado tiene radio a y está uniformemente cargada con densidad lineal de carga λ. Calcular
a) El potencial con respecto del infinito en un punto situado sobre su eje, en función la distancia x al centro de la espira.
b) A partir de la expresion del campo electrico en función de x
( problema 1.10.- y su solución ), verificar que :
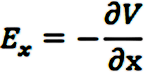
|
 |
PROBLEMA 2.9.–
Dos espiras circulares cuyo eje coincide con el eje x están uniformemente cargadas. Una tiene centro en el origen O y densidad lineal de carga λ1= 5 C/m.
La otra espira tiene centro en el punto A de abscisa xA= 8 cm y densidad de carga λ2 = 3 nC/m. Sus radios son iguales: a1 = a2= 6 cm.
En el punto A, un ión que es libre de moverse por la acción de las fuerza eléctricas, estś inicialmente en reposo.
Calcular:
a) Su velocidad cuando pasa por M, punto medio entre O y A.
b) Su velocidad cuando pasa por el punto O.
Masa del ión = 10 -26 Kg
Carga del ión = -1,6 10 -19 C
|
|
R: a) vM = 24.360 m/s b) vO = 26.904 m/s
PROBLEMA 2.10.–
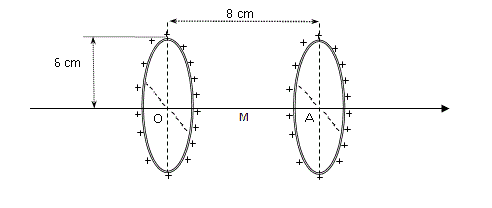
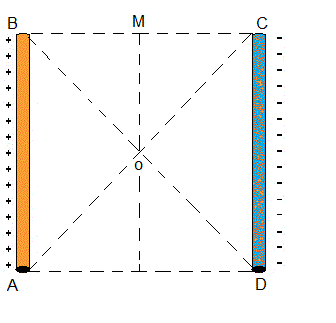
Dos varillas paralelas, uniformemente cargas, AB y CD estan enfrentadas, como indica la figura. Sus extremos forman el cuadrado ABCD con AB=BC=CD=DA= 6 cm.
La varilla AB tiene densidad longitudinal de carga λAB = 50 nC/m y la varilla CD tiene densidad longitudinal de carga λCD = -50 nC/m. Hallar el campo eléctrico y el potencial con respecto al infinito en a) El punto O, centro del cuadrado. b) El punto M, punto medio del lado BC.
|
|
R: a) EO = 42.426,4 N/C i VO = 0 b) EM = 26.832,8 N/C i VM = 0
PROBLEMA 2.11.–
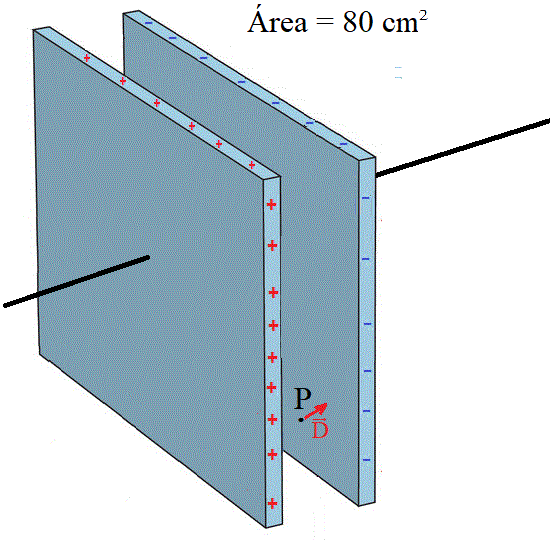
Un capacitor de placas paralelas de capacidad
C = 4 nf tiene una diferencia de potencial de 12 V entre sus placas. Estas tiene un área de 80 cm2.
Calcular:
a) El módulo del vector desplazamiento: D, en un punto P que está entre las placas.
b) El campo eléctrico y la distancia entre las placas suponiendo que entre ellas hay vacío.
c) El campo eléctrico y la distancia entre las placas suponiendo que entre ellas hay un dieléctrico de permitividad relativa εr = 8.
|
|
R: a) D = 6 μC/m2
b) E = 677.966 N/C
d = 17,7 μm c)E = 84.745 N/C d = 142 μm