E L E C T R O S T Á T I C A
Ley de Coulomb. Campo eléctrico.
En esta etapa nos proponemos calcular:
-
Fuerzas y campos de
cargas puntuales.
-
Campos de
cargas linealmente distribuidas con densidas longitudinal de carga λ.
-
Campos de
cargas superficialmente distribuidas con densidad superficial de carga σ.
-
Campos de
cargas volumétricamente distribuidas con densidad de carga volumétrica ρ.
PROBLEMA 1.1–
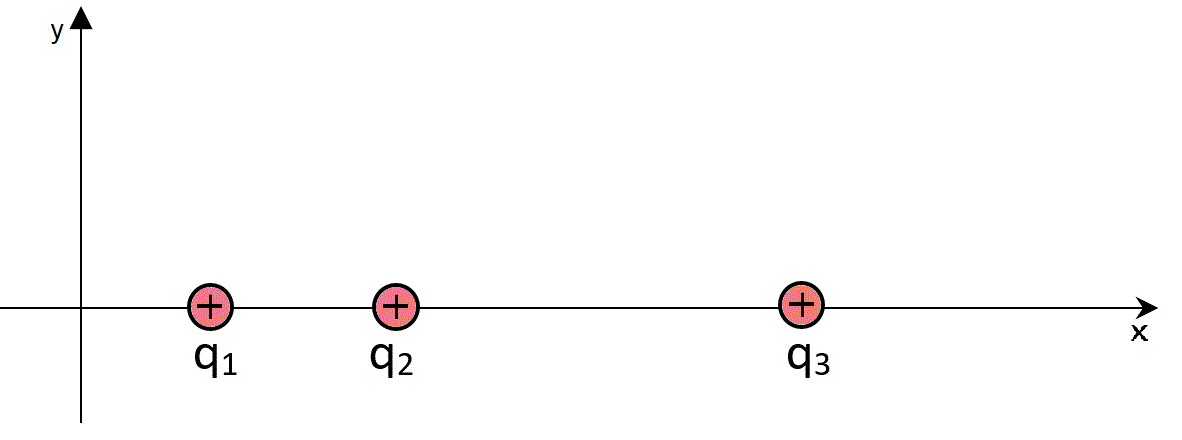
Sobre el eje x hay tres cargas puntuales positivas.
La carga q1 = 250 nC tiene abscisa x1 = 5 cm.
La carga q2 = 300 nC tiene abscisa x2 = 9 cm.
La carga q3 tiene abscisa x3 = 15 cm.
El módulo de la fuerza eléctrica sobre q3 es F3 = 0,39 N.
Hallar las fuerzas sobre las otras cargas → →
Hallar las fuerzas sobre las otras cargas F1 y F2. |
|
R: F1 = 0,51 N (-ĭ) F2 = 0,12 N ĭ
PROBLEMA 1.2–
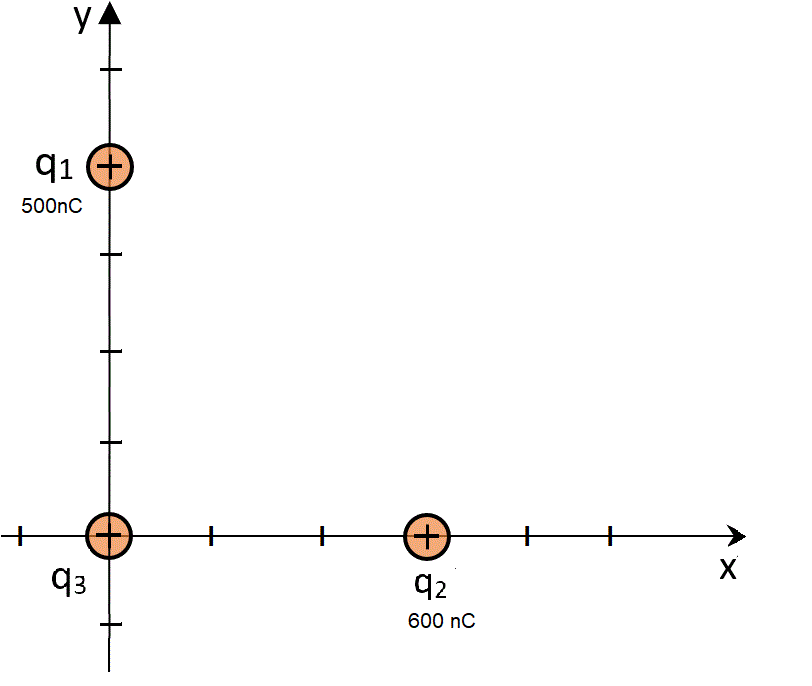
Sobre plano xy hay tres cargas puntuales positivas.
La carga q1 = 500 nC tiene coordenadas (0 ; 4 cm).
La carga q2 = 600 nC tiene coordenadas (3 cm ; 0).
La carga q3 está en el origen de coordenadas (0;0).
El módulo de la fuerza eléctrica sobre q3 es: F3 = 2,55 N.
Hallar la fuerza eléctrica sobre las otras dos cargas. |
|
R: F1 = 0,648 N (-ĭ) + 1,9463 N jˇ
F2 = 2,9569 N ĭ + 0,864 N (-jˇ)
PROBLEMA 1.3–
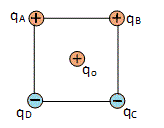
El cuadrado ABCD tiene 20 cm de lado. En en cada uno de sus vértices hay una carga puntual: qA = 8nC, qB = 8 nC, qC = -8 nC y qD = -8 nC . Además en el centro del cuadrado hay un carga qO.
Se desea que la fuerza sobre la carga qo sea nula. Para ello se coloca una carga qP en uno de los lados del cuadrado. Indicar cual es la posición y el valor de qP que hace que la fuerza sobre qO sea nula. Justificar la respuesta y su unicidad |
|
R: qP = 11,31371 nC
PROBLEMA 1.4–
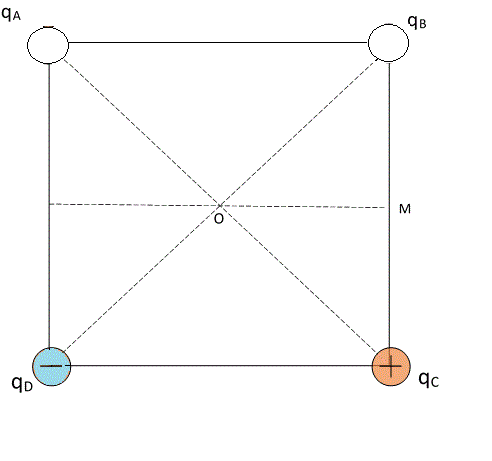
En los vértices del cuadrado ABCD de 20 cm de lado hay cuatro cargas puntuales qA, qB, qC y qD.
El campo eléctrico en el centro O del cuadrado vale cero: Eo = 0.
Si qC = 10 nC y qD = -10 nC.
a) ¿ Cuánto valen qA y qB ?
b) En esas condiciones cuánto vale el campo eléctrico en M: punto medio del lado BC. |
|
→
R:
E M = 16.390 N/C jˇ
PROBLEMA 1.5–
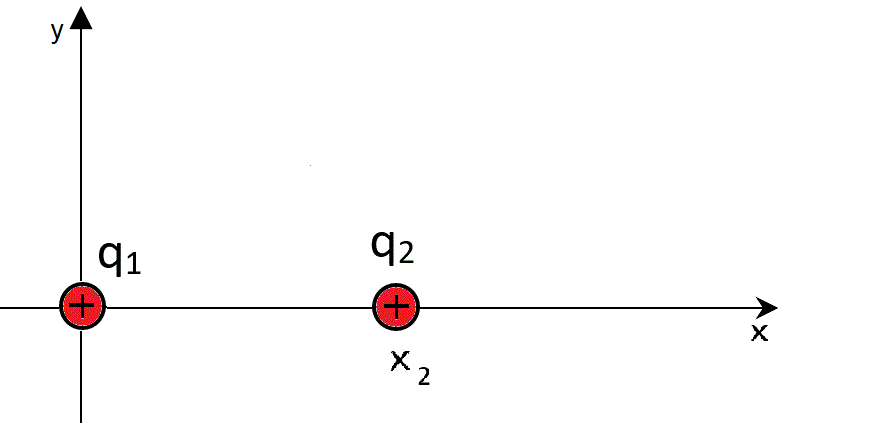
| En el eje x hay dos cargas puntuales del mismo signo: q1 = 40 nC y q2 = 10 nC. La carga q1 está el origen de coordenadas y la carga q2 tiene abscisa x2 = 12 cm. Encontrar las coordenadas de el o los puntos en los que el campo eléctrico se anula. |
|
R: a) x = 8 cm Ambas cargas tiene igual signo y valen:; b) x = 36 cm
PROBLEMA 1.6–
|
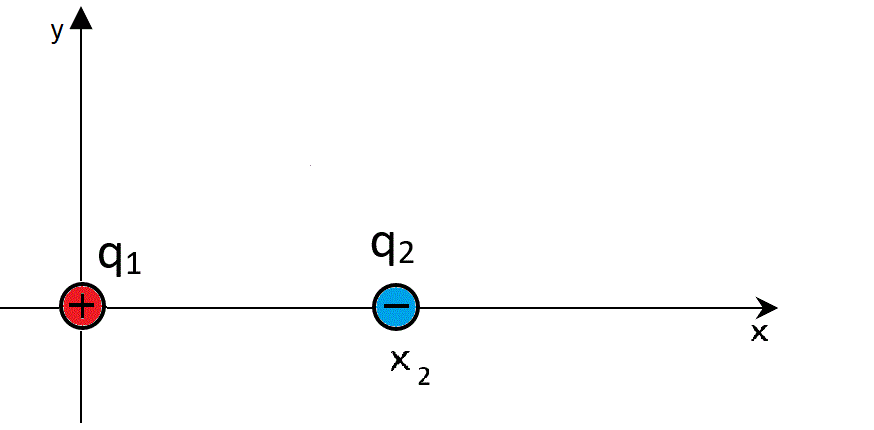
En el eje x hay dos cargas puntuales de distinto signo: q1 = 40 nC y q2 = -10 nC. La carga q1 está el origen de coordenadas y la carga q2 tiene abscisa x2 = 12 cm.
a) Encontrar las coordenadas de el o los puntos en los cuales el campo eléctrico se anula.
b) Para pensar:
Analice los valores del campo eléctrico a lo largo del eje. x.
¿Tiene máximos relativos? si-no-¿Porquè? |
|
R: a) En x = 24 cm el campo vale cero. b) E vale 0 en x = 24 cm y tiende a 0 en x → ∞. Entonces ...
PROBLEMA 1.7–
|
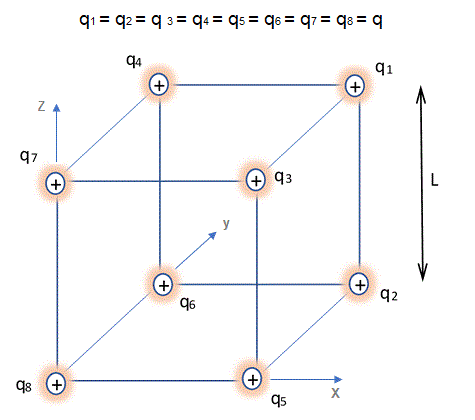
En cada uno de los vértices de un cubo de lado L hay cargas puntuales q. Expresar en función de L y q :
a) el módulo del campo electrico en el centro del cubo.
b) el módulo del campo electrico en el centro una de las caras.
c) el módulo de la fuerza sobre cada carga. |
d) el módulo del campo eléctrico en el centro si se quita una de las cargas.
|
R:
a) 0
b) 8/3 √(2/3) K q/L2 = 2,18 K q/L2
c) (√3 + √6 /2 + 1/3)KVq2/L2 = 3,29 K q2/L2
d) 4/3 K q/L2
PROBLEMA 1.8–
|
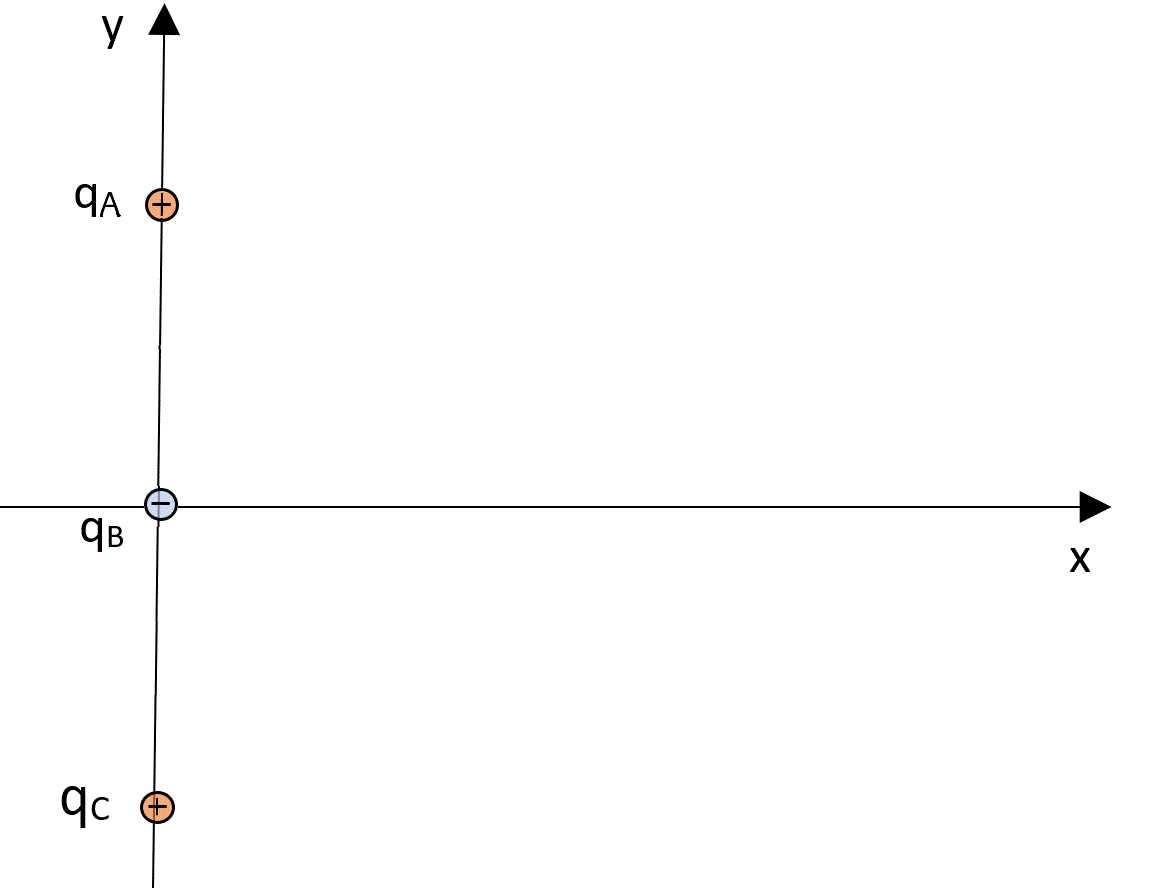
Sobre el eje "y" hay tres cargas puntuales: qA = qC = 99 nC, qB = -70 nC. Sus ordenadas son: yA = 12 cm, yB = 0, yC = -12 cm.
Encontrar los puntos del eje x donde el campo eléctrico es cero. |
|
R: x = ±12 cm
PROBLEMA 1.9–
|
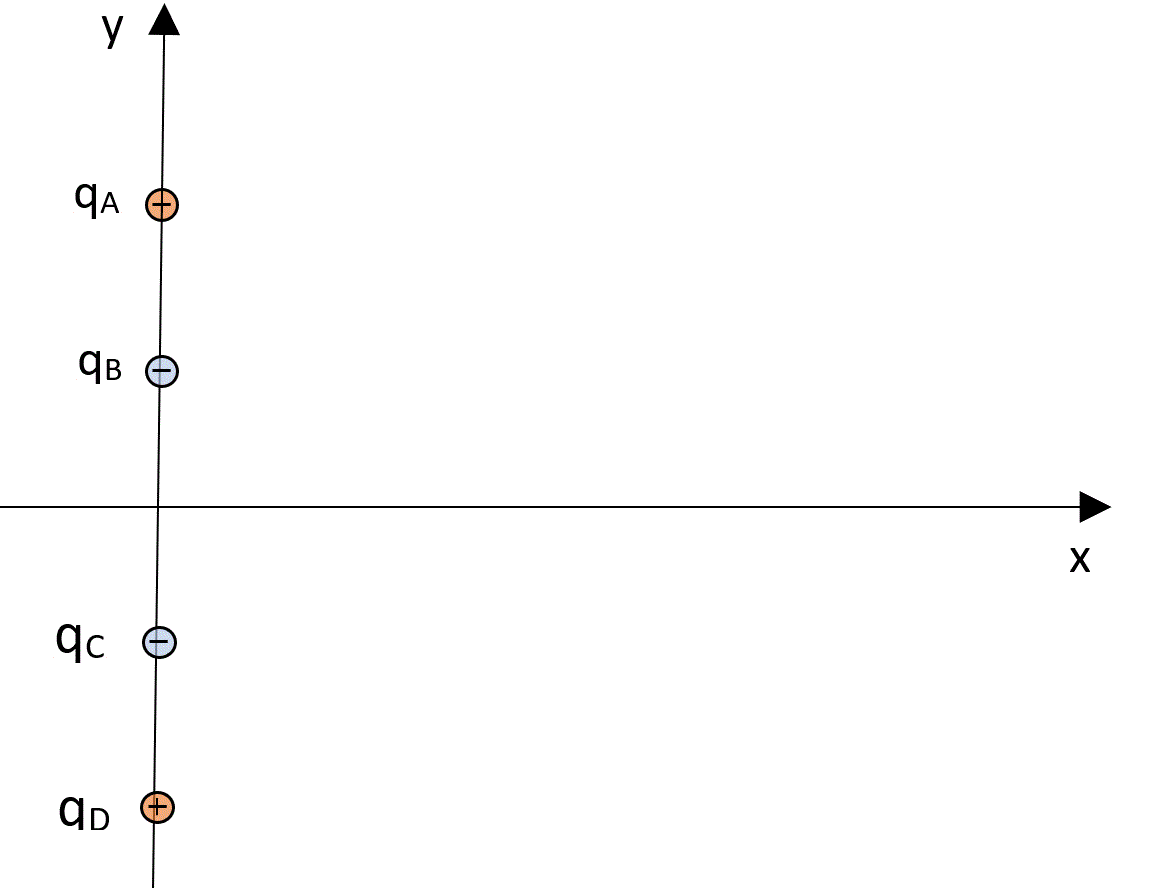
Sobre el eje "y" hay cuatro cargas puntuales:
qA = qD = 64 nC.
qB = qC = -27 nC
Sus ordenadas son: yA = 16 cm, yB = 9 cm, yC = -9 cm, yD = -16 cm.
Encontrar los puntos del eje x donde el campo eléctrico es cero. |
|
R: x = ±12 cm y x = 0
Cargas linealmente distribuidas
λ uniforme |
PROBLEMA 1.10–
|
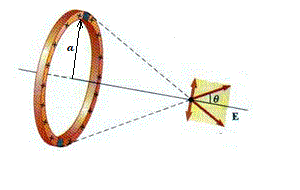
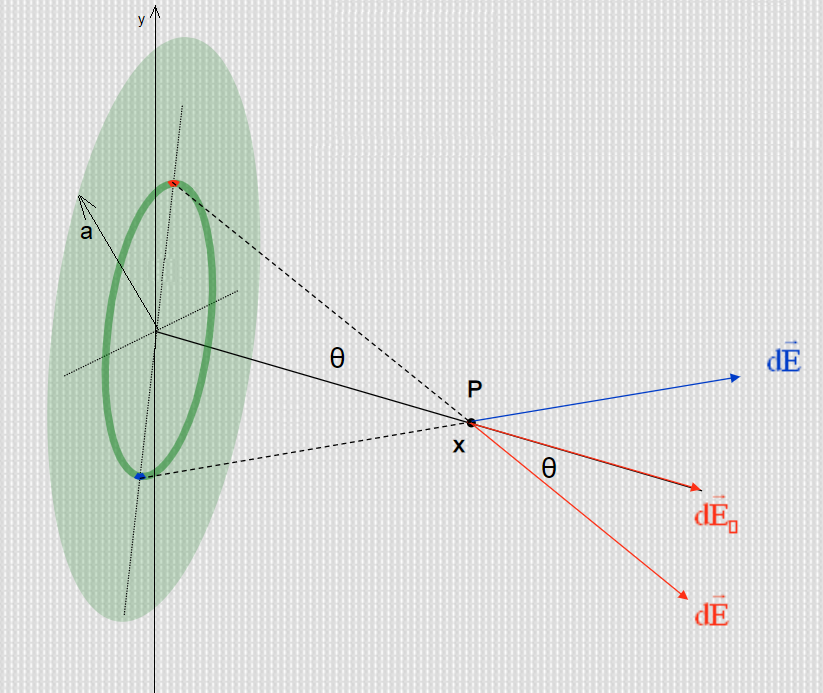
Una espira circular de alambre delgado tiene radio a, centro en el origen y densidad lineal de carga λ.
Calcular la expresión del campo eléctrico en un punto situado sobre el eje de la espira, en función de su distancia x al centro. |
|
PROBLEMA 1.11–
|
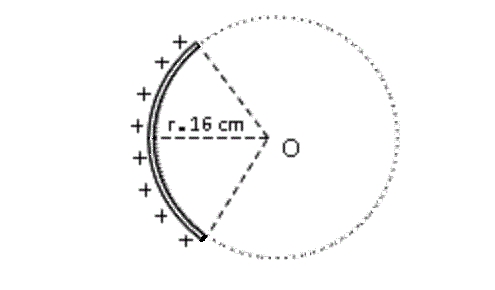
Un arco de circunferencia tiene una carga eléctrica total q = 80 nC uniformemente distribuida a lo largo de su longitud. Su radio es de 16 cm y abarca un ángulo de 50o.
Hallar el campo eléctrico en el centro O.
|
|
R: EO = 27.241 N/C
PROBLEMA 1.12–
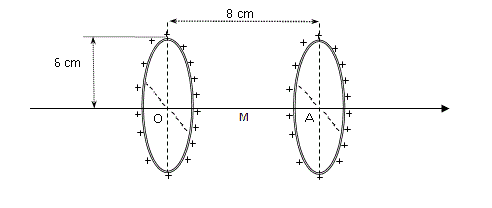
Dos espiras circulares cuyo eje coincide con el eje x están uniformemente cargadas. Una tiene centro en el origen O y densidad lineal de carga λ1= 3 nC/m.
La otra espira tiene centro en el punto A de abscisa xA= 8 cm y densidad de carga λ2 = 5 nC/m. Sus radios son iguales: a1 = a2= 6 cm.
Calcular:
a) El módulo del campo eléctrico en el punto A.
b) El módulo del campo eléctrico en el punto O.
c) El módulo del campo eléctrico en M, (punto medio entre O y A). |
|
R: a) EA = 814,3 N/C b) EO = 1357,168 N/C c) EM = 723,86 N/C
PROBLEMA 1.13–
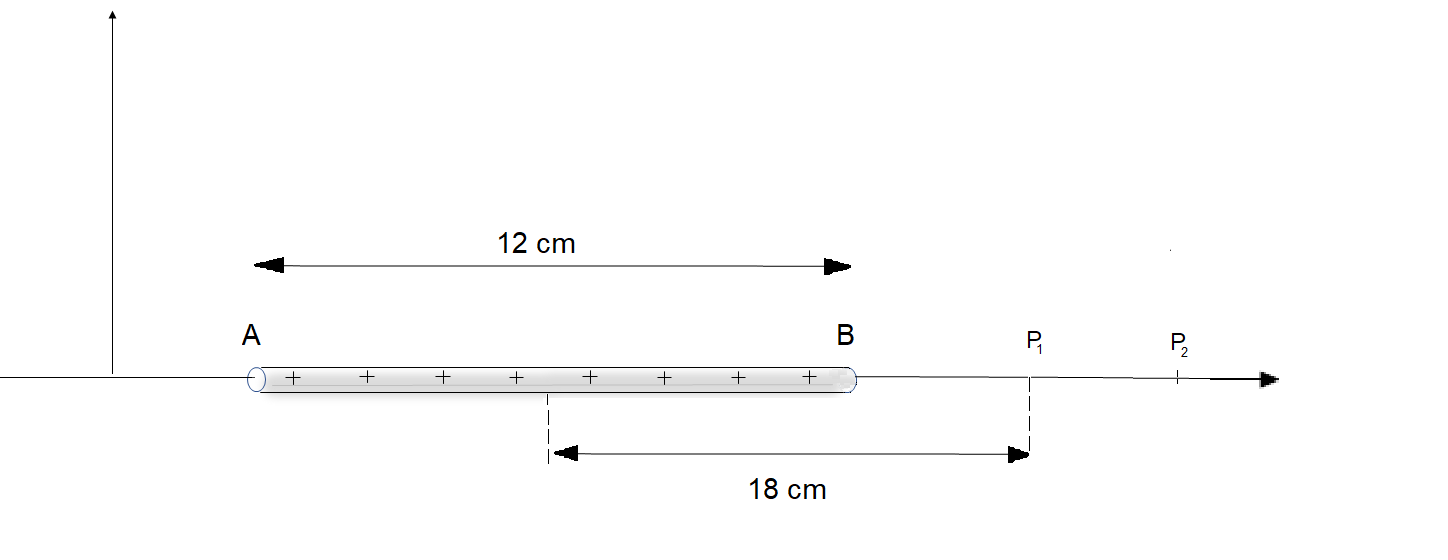
Una varilla delgada tiene una carga eléctrica uniforme λ = 4 nC/m a lo largo de toda su longitud. La varilla tiene 12 cm de largo. El punto P1 se encuentra sobre el eje de la varilla a una distancia 18 cm hacia la derecha del punto medio. El punto P2 se encuentra sobre el eje de la varilla a una distancia 25 cm de su punto medio también a la derecha. En el punto P1 se coloca un ion positivo en reposo.Teniendo en cuenta que el ión se mueve solo por la sola acción de las fuerzas eléctricas, se pide calcular:
a) La aceleración del ión cuando pasa por el punto P1.
b) La aceleración del ión cuando pasa por el punto P2.
Justificar a partir de las leyes básicas de la electricidad.
Masa del ión = 4 . 10 ˉ24 Kg. Carga del ión = 1,6 . 10ˉ19 C |
|
R: a) a = 6 . 106 m/s2
b) a = 2,93 . 106 m/s2
PROBLEMA 1.14–
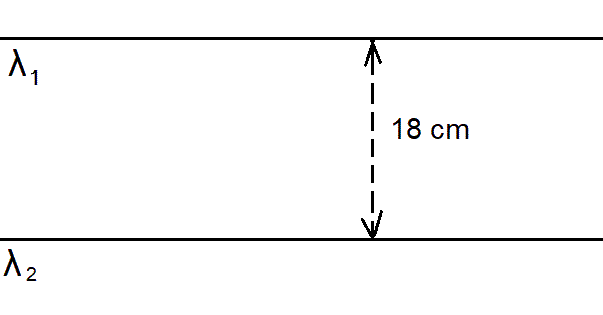
Dos conductores delgados rectos infinitos uniformemente cargados son paralelos y están a 18 cm de distancia entre sí. El conductor uno tiene densidad de carga λ1 = 200 nC/m y el conductor dos λ2 = 400 nC/m. Determinar:
a) Los puntos donde el campo eléctrico es cero.
b) El campo eléctrico en los puntos que se encuentran fuera del plano del dibujo, 4 cm por encima de los puntos hallados en (a) |
|
R: a) Los que están a 6 cm del conductor uno y a 12 cm del conductor 2
b) F = -23089,6 N/C (-ĭ) + 68524,14 N/C (jˇ)
Cargas linealmente distribuidas
λ no uniforme |
PROBLEMA 1.15–
|
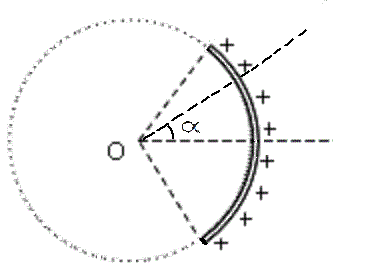
Un arco de circunferencia de radio r = 20 cm. abarca un ángulo de 90o (de -45o a +45o).
A lo largo de su longitud tiene una densidad lineal de carga variable que, en función del ángulo central α, vale:
λ(α) = λ0 cos α
donde λ0 = 300 nC/m
Hallar el campo eléctrico en el centro O.
|
 |
R: E =1/(4 π ε0) . λ0/r .(π/2 + 1/2) = 17.352,5 N/C
PROBLEMA 1.16–
|
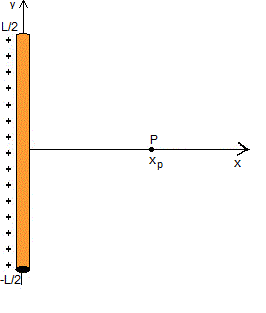
Una varilla delgada tiene longitud L. Su punto medio coincide con el origen y y sus extremos estan sobre el eje "y". A lo largo de su longitud, la densidad de carga está dada por: λ(y) = λo. |y|
Hallar el campo eléctrico en el punto P de coordenadas (xp;0;0) en funcion de xp, L y λo
|
 |
R: E =1/(2 π ε0) . λ0 . xp /(xp2 + L2/4)1/2
Cargas distribuídas superficiales
σ uniforme |
PROBLEMA 1.17–
Un disco circular delgado, uniformemente cargado con densidad superficial de carga σ tiene radio a, centro en el origen y su eje coincide con el eje x.
Calcular la expresión del campo eléctrico en un punto situado sobre el eje, en función de su distancia x al centro.
Sugerencia: dividir el disco en anillos
concéntricos de radio r y ancho dr. |
|
|
R: E = σ/2ε0 . [1 - x / ( x2 + a2 )(1/2)]
PROBLEMA 1.18–
Una esfera conductora tiene radio RE = 10 cm.
Sobre su superficie hay una densidad de carga σ = 120 nC/m2. Calcular el módulo del campo electrico en:
a) Un punto A, que está a 25 cm del centro.
b) Un punto B, que está a 5 cm del centro.
|
|
R: a) EA = 2171,469 N/C b) EB = 0
PROBLEMA 1.19–
Un cilindro conductor tiene radio RC = 20 cm.
Sobre su superficie hay una densidad de carga σ = 250 nC/m2. Calcular el módulo del campo electrico en:
a) Un punto A, que está a 40 cm del eje .
b) Un punto B, que está a 15 cm del eje
|
|
.
R: a) EA = 141.24,3 N/C b) EB = 0
PROBLEMA 1.20–
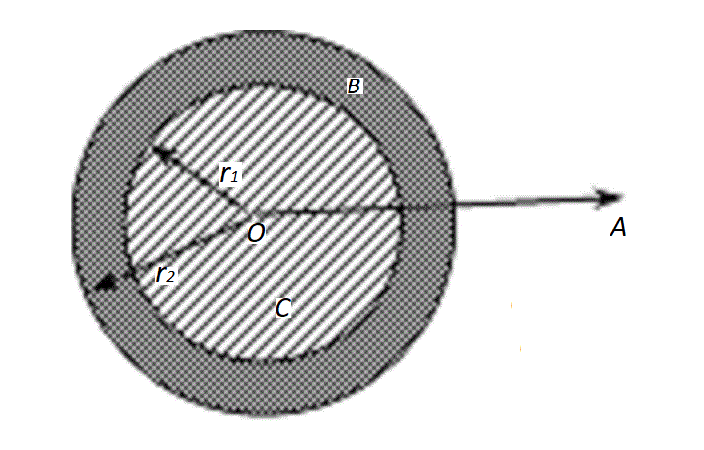
| Una esfera conductora cargada, de radio r1 = 5 cm, está recubierta por una capa de goma que forma una esfera hueca de radio exterior r2 = 8 cm. En el punto A, que está a 9 cm del centro O, el campo eléctrico tiene dirección saliente y módulo EA = 20.000 N/C. La constante dieléctrica relativa de la goma es k = 6.
Hallar:
a) El valor de carga Q de la esfera conductora central.
b) El módulo del campo eléctrico en el punto B que está a 6 cm de distancia del centro O
c) El módulo del campo eléctrico en el punto C que está a 2 cm de distancia del centro O.
|
|
R: a) Q = 18 nC b) EB = 7.500 N/C c) EC = 0
Cargas distribuídas en un volumen
ρ uniforme |
PROBLEMA 1.21–
Una esfera no-conductora tiene radio RE = 10 cm.
En todo sus puntos tiene densidad volumétrica de carga ρ = 400 nC/m3. Calcular el módulo del campo electrico en:
a) Un punto A, que está a 25 cm del centro.
b) Un punto B, que está a 5 cm del centro.
|
|
R: a) EA = 241,27 N/C b) EB = 754 N/C
PROBLEMA 1.22–
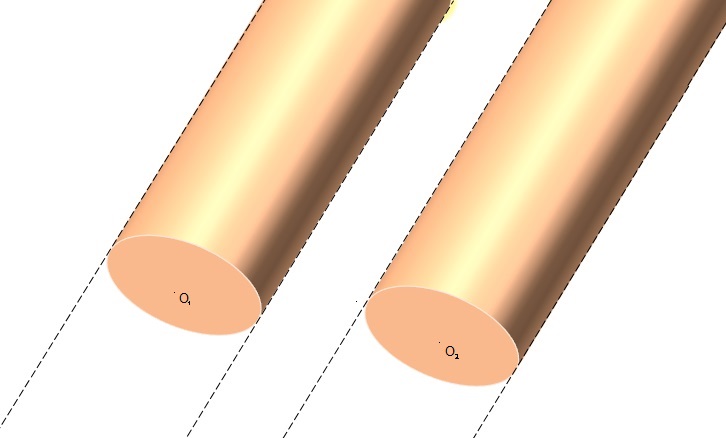
Un sistema está compuesto por dos esferas no-conductoras de radios: R1 = R2 = 2 cm.
La esfera con centro en el punto O1 tiene densidad de carga volumétrica uniforme ρ1 = 400 nC/m3.
La esfera con centro en el punto O2 tiene densidad de carga volumétrica uniforme ρ2 = 250 nC/m3.
La distancia entre los centros es O1O2 = 8 cm.
Aplicando la ley de Gauss y el principio de superposición calcular el módulo del campo eléctrico en O1 y en O2. Para pensar:
¿ Con qué fuerza las esferas se repelen entre sí ? JUSTIFICAR |
|
R: a) E1 = 11,781 N/C b) E2 = 18,85 N/C
PROBLEMA 1.23–
Un sistema está compuesto por dos cilindros paralelos no-conductores de radios: R1 = R2 = 2 cm.
El cilindro uno tiene densidad de carga volumétrica uniforme ρ1 = 400 nC/m3 y el cilindro dos tiene densidad de carga volumétrica uniforme ρ2 = 250 nC/m3. La distancia entre sus ejes es 8 cm.
Aplicando la ley de Gauss y el principio de superposición: calcular:
a) El módulo del campo eléctrico en los puntos del eje del cilindro uno.
b) El módulo del campo eléctrico en los puntos del eje del cilindro dos.
|
|
R: a) E1 = 58,9 N/C b) E2 = 113,1
N/C