.
.
.
.
Calcular la corriente que circula por el inductor en función del tiempo si la llave se cierra en t = 0.
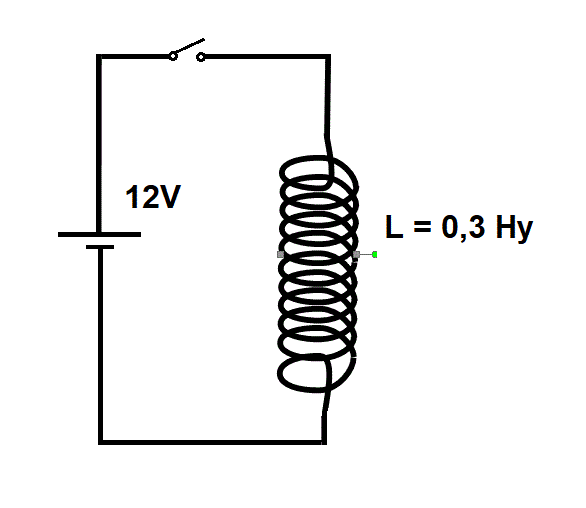
R: i(t) = 40 A/s . t
Calcular la corriente que circula por el inductor en función del tiempo si la corriente inicial es i(0) = 2 A.
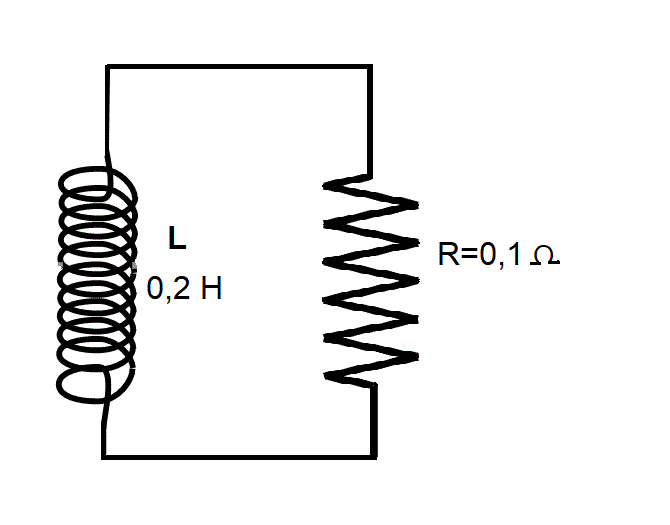
R: i(t) = 2 A e-t/2s
En el circuito de la figura un solenoide ideal de inductancia L = 1,5 H está conectado a una fuente ideal de 12 V a través de una llave. Además hay una resistencia de R = 0,5 Ω en paralelo con L. Cerramos la llave durante 10 segundos. Digamos que está abierta y en t = -10 seg la cerramos y en t = 0 la abrimos nuevamente. Calcular
a) La corriente en el solenoide para t igual a -8, -5, -2, 0, 1, 2 y 3 segundos.
b) La corriente en la resistencia en esos instantes excepto en cero
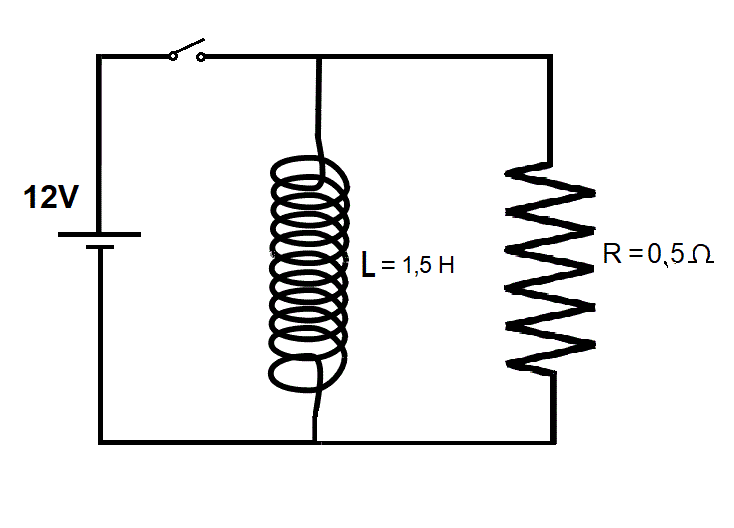
R: a) i(-8s)=16 A i(-5s)=40 A i(-2s)=64 A i(0)=80 A i(1s)=80 A e-1/3 i(2s)=80 A e-2/3 i(3s)=80 A e-1
b) i(-8s)=-24 A i(-5s)=-24 A i(-2s)=-24 A i(1s)=80 A e-1/3 i(2s)=80 A e-2/3 i(3s)=80 A e-1
En el circuito de la figura el capacitor está inicialmente descargado.
En el instante t = 0 se cierra el interruptor.
Calcular:
a) La tensión en el capacitor, la tensión en la resistencia y la corriente en t = 0.
b) La tensión en el capacitor, la tensión en la resistencia y la corriente cuando el tiempo tiende a infinito.
c) La tensión en la resistencia y la corriente en t = 0,4 segundos y en t = 0,6 segundos.
d) La tensión en el capacitor en t = 0,4 segundos y en t = 0,6 segundos
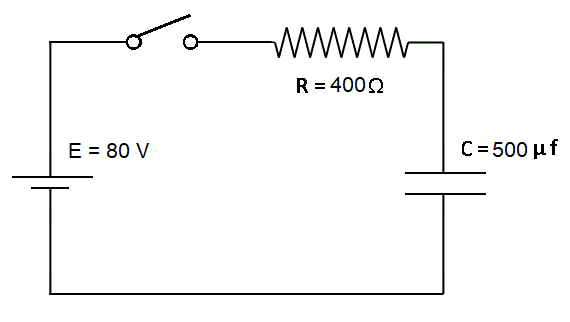
R: a) Vc(0) = 0 VR (0) = 80 V
b) t→∞ Vc = 80 VR = 0
c) VR (0,4 s) = 10,82V i(0,4s) = 27 mA
VR (0,6s) = 4V i(0,6s) = 10 mA
d) Vc (0,4s) = 69,18 V Vc (0,6s) = 76,017 V
En el circuito de la figura el interruptor está inicialmente cerrado y se lo abre en el instante t = 0 .
Calcular la tensión en el capacitor y la corriente en la resistencia en:
a) t = 0.
b) cuando el tiempo tiende a infinito.
c) en t = 0,6 segundos.
d) en t = 1,8 segundos
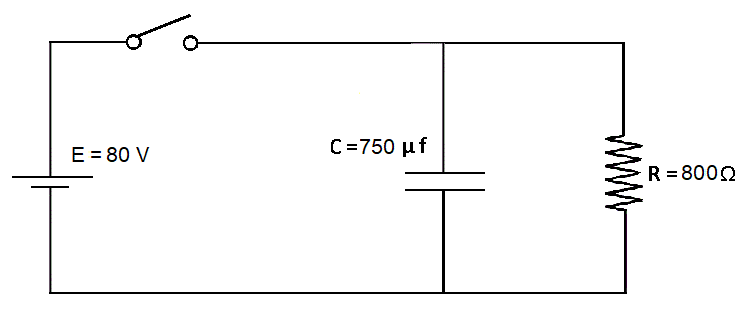
R: a) Vc(0)= 80 V i(0) = 0,1 A b) t→∞ Vc = 0 i = 0 c) Vc(0,6s) = 29,43 V i(0,6s) = 0,0368 A d) Vc(1,8s) =4 V i(1,8s) = 5 mA