El circuito plano de la figura contiene dos conductores infinitos, conectados por un arco de circunferencia de 315o y radio r = 8 cm. Por ellos circula una corriente i = 25 A.
Calcular el campo magnético en el punto O, centro del arco. (módulo dirección y sentido), indicando la contribución al campo total de cada tramo del circuito.
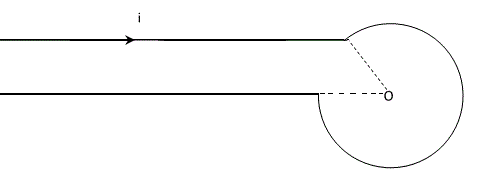
R: BO = 171,8 μT + 12,95 μT = 184,75 μT
En la figura se ven dos conductores semi‑infinitos con corriente i1 = 4 A unidos por una semi‑circunferencia de radio r1 = 5 cm
Calcular la corriente que debe circular por la espira más pequeña de radio r2 = 2 cm para que en el punto O el campo magnético sea cero.
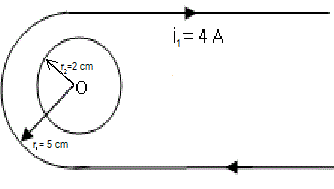
R: i = 1,309 A
Una espira circular con centro en el centro de coordenadas O, está en el plano yz ( su eje es el eje x). Su radio es r = 3 cm. Conduce una corriente i = 8 A que vista desde las x positivas tiene sentido horario. Calcular:
a) El campo magnético en el punto P de coordenadas: x = 4 cm ; y = 0 ; z = 0
b) La fuerza magnética que se ejerce sobre una partícula de carga q = 7 nC que pasa por ese punto P moviéndose en dirección y a una velocidad v = 300 m/s j . Indicar módulo, dirección y sentido.
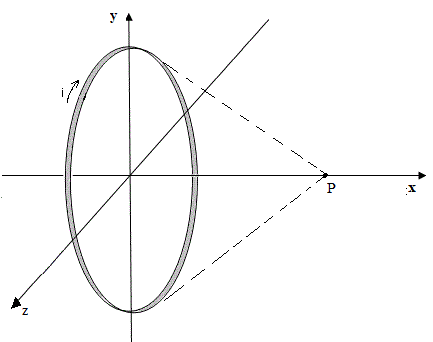
R: a) BP = 36,19 μT
Por los conductores infinitos circula una corriente de 2 A en el sentido indicado y por la espira circular circula una corriente de 1 Amper. Calcular:
a) El campo magnético en el punto O, centro de la espira.
b) El campo magnético en un punto P que está, en el eje de la espira, a 10 cm de altura por encima del plano del dibujo.
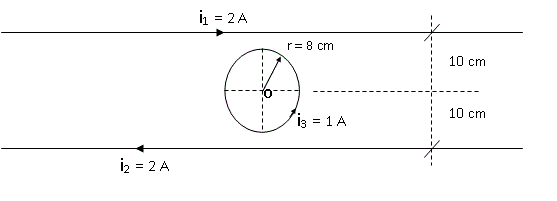
R: a) Bo = 8 μT - 7,584 μT = 0,155 μT b) Bo = 4 μT - 1,91 μT = 2,09 μT
En la figura vemos dos conductores horizontales rectos semi‑infinitos unidos por un arco AB, dos segmentos rectos y dos tramos rectos por los cuales circula una corriente i = 24 A. El arco AB tiene centro en punto O y recorre un angulo de 40o a cada lado de la vertical.Calcular el campo magnético en el punto O (dirección, modulo y sentido).
Radio del arco r = 25 cm
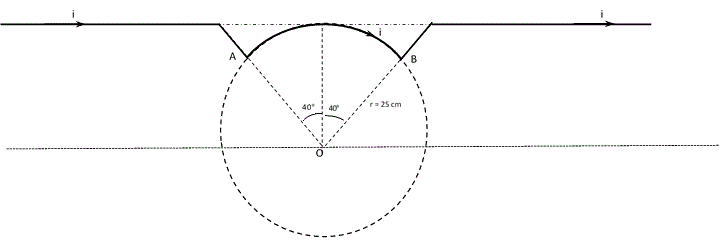
R: Bo = 6,86 μT + 13,4 μT = 20,26 μT
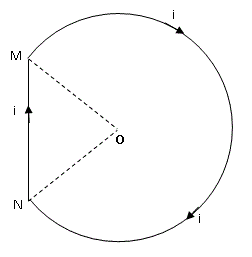
En la figura se observa un arco de circunferencia MN que se cierra con una varilla conductora NM Por ellos circula una corriente de i = 18 A.
OM es perpendicular a ON.
Radio = OM = ON = 20 cm
Calcular el campo nagnético en O.
Justificar.
R: Bo = 4,24 10-5;T + 18 μT = 60,4 μT
El circuito ABCD de la figura conduce una corriente de i = 15 A.
PD = DA = DC = 5 cm
Aplicando la ley de Boit-Savart, hallar el vector campo magnético en el punto P.
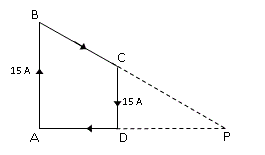
R: BP = 10,6 μT
Por los vértices del cuadrado ABCD pasan cuatro conductores rectos, infinitos, perpendiculares al plano del dibujo. Las cuatro corrientes son entrantes iA=iB = iC = iD = 8 Amperes.
AB = BC = CD = DA = 20 cm. Calcular:Tema 1
a) El campo magnetico en el punto O, centro del cuadrado.
b) El campo magnetico en el punto M, punto medio del lado BC.
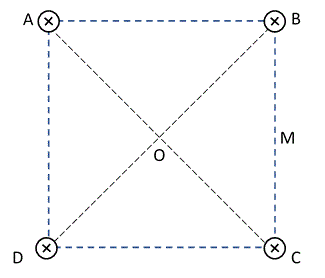
R: a) BO = 0; b) BM = 12,8 μT
Repetir el problema anterior con son iA = iB entrantes e iC = iD salientes.
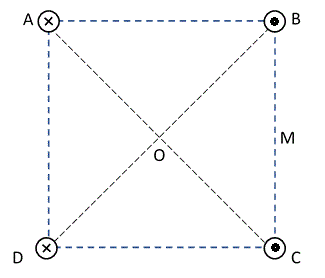
R: a) BO = 32 μT ; b) BM = 12,8 μT