La varilla conductora MN de la figura tiene longitud l = 40 cm y se mueve hacia la derecha con una velocidad v = 50 m/s. En todo el espacio en el cual se mueve hay un campo magnético uniforme B = 0,3 T que, en todo momento, es perpendicular a la varilla y a su velocidad y tiene sentido entrante al plano del dibujo. Calcular:
a) La diferencia de potencial ( f.e.m. ): VM-VN. Justificar
b) ΏCómo se puede conectar un voltímetro para medir esa diferencia de potencial? Hacer un esquema.
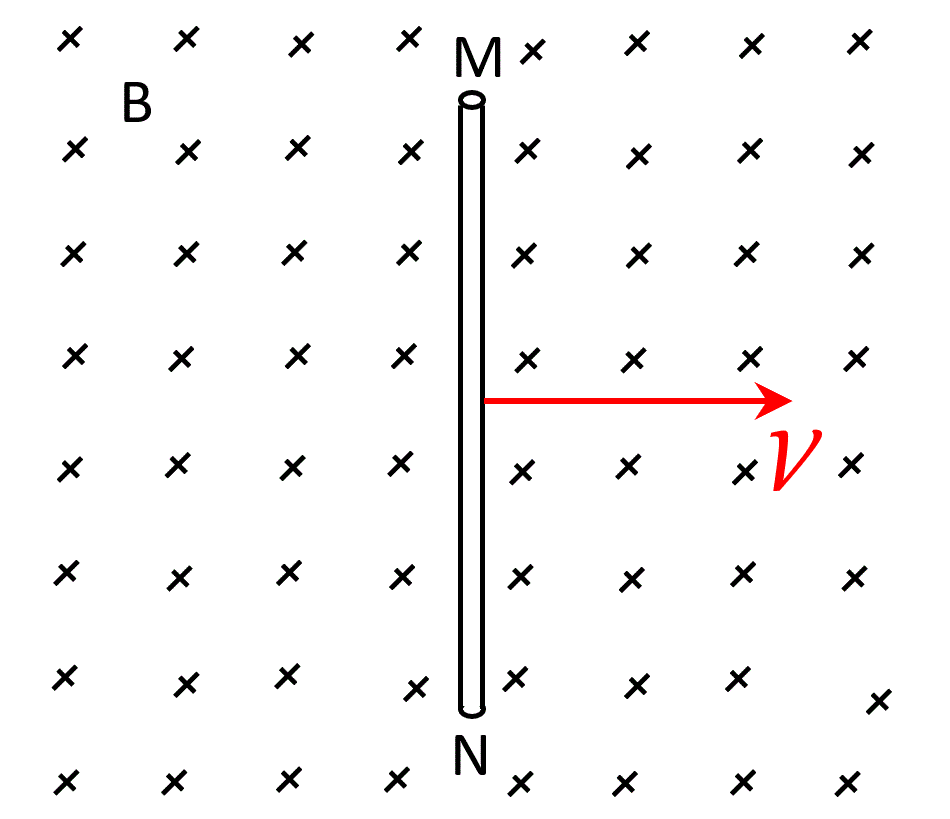
R: f.e.m.= 6 V
La varilla MN se mueve a una velocidad de 120 m/s dentro de un campo magnético uniforme B = 0,8 T perpendicular al plano del dibujo con dirección entrante. El circuito tiene resistencia R = 0.3 Ω. Calcular:
a) La diferencia de potencial ( f.e.m. ):
VM - N. Justificar
b) La intensidad de corriente.
c) La energía que disipa R en 5 segundos.
d) La fuerza magnética en la varilla (módulo dirección y sentido)
e) El trabajo que realiza en 5 seg.
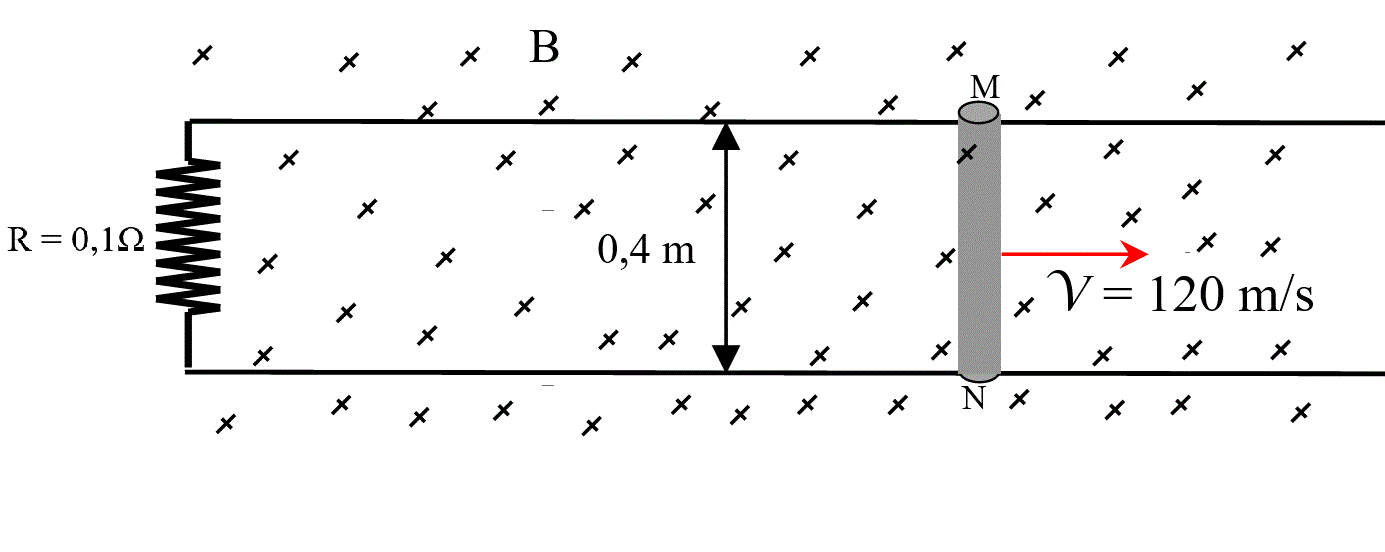
R: a) VM - VN. = 38,4 V b) i = 128 A c) 24.576 Joules d) F = 40,96 N e) 24.576 Joules
La varilla conductora MN de la figura tiene longitud l = 40 cm y estα girando, a razón de 60 vueltas por segundo en sentido antihorario, alrededor del punto N. En todo el plano de rotación hay un campo magnético uniforme B = 0,3 T perpendicular al plano con sentido saliente.
a) Calcular la diferencia de potencial (f.e.m) VM-VN Justificar
b) Calcular nuevamente VM-VN si la varilla gira alrededor del punto P
situado a 10 cm de N ( y a 30 cm de M) en lugar de hacerlo alrededor del extremo M.
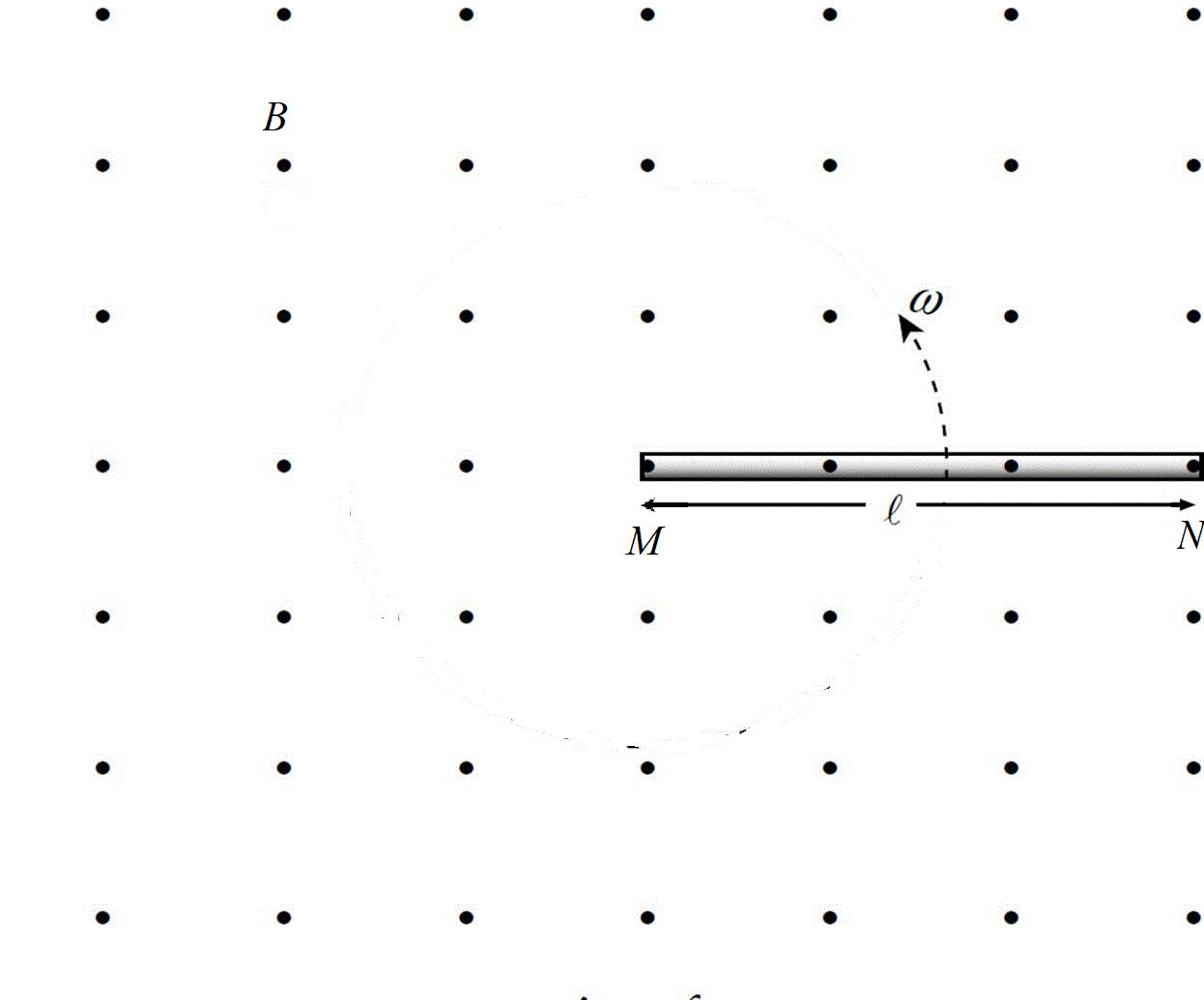
R: a) VM-VN = 9.05 V b) VM-VN = 4.52 V
La espira rectangular de la figura gira a razón de 3000 revoluciones por minuto dentro de un campo magnético uniforme B. El campo B es perpendicular el eje de rotación de la espira y forma un ángulo de 60o con la horizontal. La fuerza electromotriz inducida en dicha espira es registrada por el voltímetro V a través de contactos deslizantes que están sobre el eje. Hallar esa tensión V(t) en función del tiempo sabiendo que la espira inicialmente se encuentra en posición horizontal.
Datos;
Área de la espira A= 900 cm2
Campo magnético B = 0,2 T
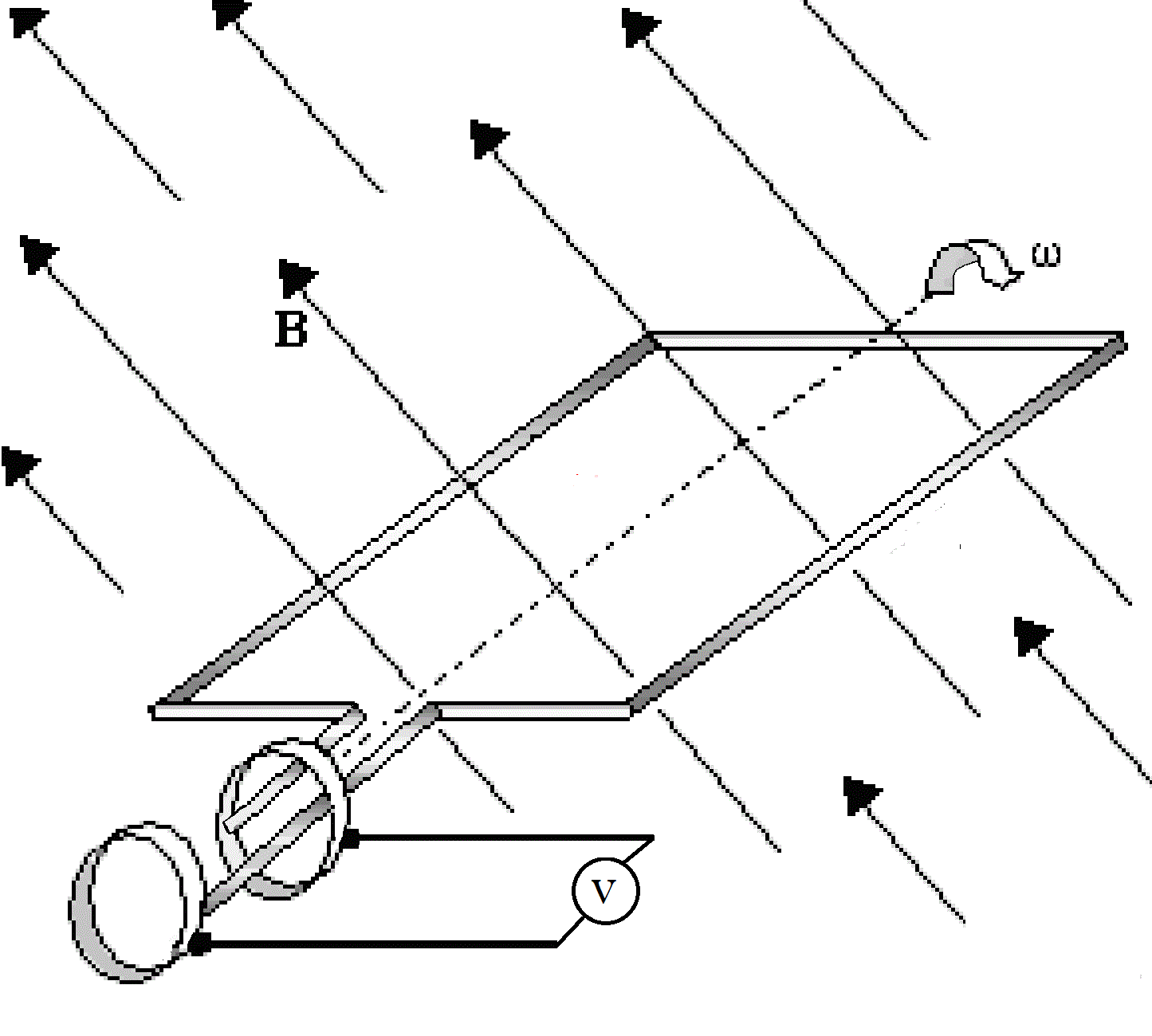
R: v(t) = 5,655 V cos( 314 1/s t - π/3)
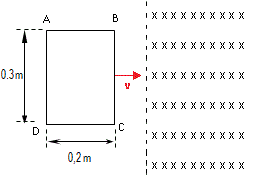
La espira rectangular ABCD se mueve hacia la derecha con una velocidad v = 200 m/s. y en el instante t = 0 el lado BC penetra en una zona de campo magnético uniforme entrante B = 0,5 T. La espira rectangular tiene una resistencia R = 2 Ω ?
Calcular la f.e.m., la corriente i y la fuerza neta F en la espira, para:
a) t negativo
b) t positivo menor que 0,001 segundos
c) t mayor que 0,001 segundos
d) Graficar esas tres variables en función del tiempo.
R: a) f.e.m = 0 , i = 0 , F = 0 b) f.e.m = 30 V , i = 15 A , F = 2,25 N c) f.e.m = 0 , i = 0 , F = 0
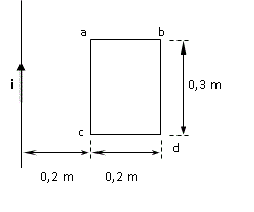
La corriente en el alambre infinito de la figura vale i1 = 25 A.
Calcular la f.e.m. inducida en la espira rectangular si ésta tiene una velocidad v = 40 m/s con dirección:
a) hacia arriba
b) hacia la derecha
Indicar, en cada caso, el sentido de la corriente inducida.
R: a) f.e.m. = 0 b) f.e.m. = 150 μV i2 con sentido horario
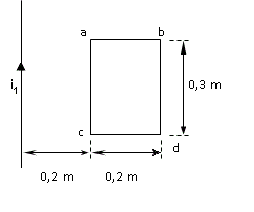
La corriente en el alambre infinito en función del tiempo vale: i1(t) = 0,5 A/s t
Calcular:
a) El flujo generado en la espira rectangular en t = 2 seg.
b) El flujo en la espira rectangular en función del tiempo.
c) La fuerza electromotriz inducida en la espira rectangular en función del tiempo.
d) El sentido de la corriente inducida en la espira i2.
R: a) Φ(2 seg) = 4,16 10-8 ;Wb b) Φ(t) = 2,08 10-8 Wb/s . t c) f.e.m. = 2,08 10-8 V d) antihoraria
Alrededor del solenoide de la figura se han arrollado tres espiras de alambre conductor. El solenoide tiene 30 cm de largo con un total de 1200 espiras.
El área de su sección es de 4 cm2.
Por el solenoide circula una corriente:
i(t) = 1,5 A sen (300 1/s t )
Calcular la diferencia de potencial ΔV(t) entre los bornes A y B en función del tiempo. Justificar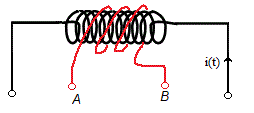
R: VA -VB = 0,002714 V cos(300 1/s . t)
El toroide de sección rectangular de la figura tiene 300 espiras. Alrededor del mismo se han arrollado tres espiras de alambre conductor. Aplicando las leyes básicas del magnetismo hallar la inductancia mutua entre el toroide y las tres espiras.
Radio interior del toroide r1 = 3 cm
Radio exterior del toroide r2 = 5 cm
Alto h = 1,2 cm
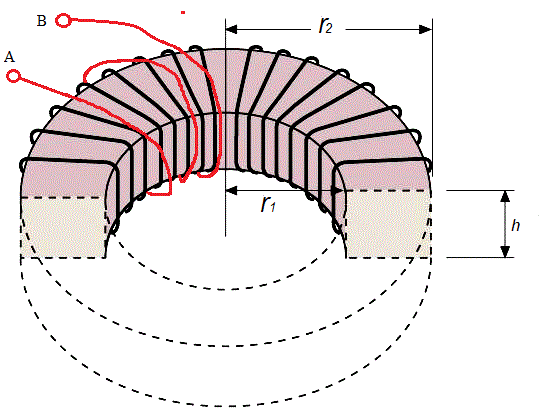
R: L12 = 1,1 μHy
El solenoide de la figura tiene 30 cm de largo con un total de 1200 espiras.
El área de su sección es de 4 cm2.
Por el solenoide circula una corriente:
i(t) = 1,5 A sen (300 1/s t )
Calcular la diferencia de potencial ΔV(t) entre los bornes A y B en función del tiempo. Justificar
R: VA -VB = 1,086 V cos(300 1/s . t)
El toroide de sección rectangular de la figura tiene 300 espiras por las que circula una corriente creciente:
i(t) = 9 A/s t (rampa de corriente).
Aplicando las leyes básicas del magnetismo calcular:
a) Su auto-inductancia.
b) La f.e.m. entre sus bornes
Radio interior del toroide r1 = 3 cm
Radio exterior del toroide r2 = 5 cm
Alto h = 1,2 cm
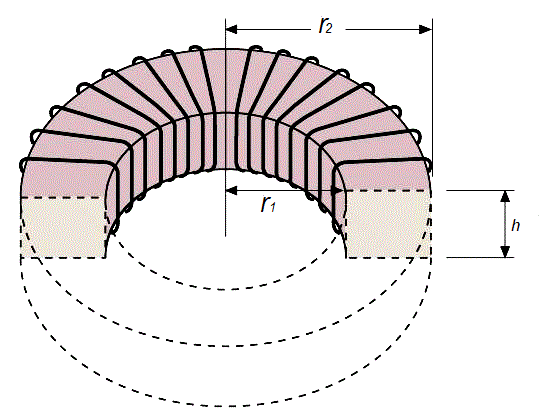
R: L = 110 μHy
El solenoide de la figura tiene largo L = 40 cm y un total de 2400 espiras. El área de su sección es de 8 cm2.
En t = 0 se cierra la llave que la conecta a una fuente ideal de 12 V.
Calcular la corriente en función del tiempo: i(t) para t > 0. Justificar
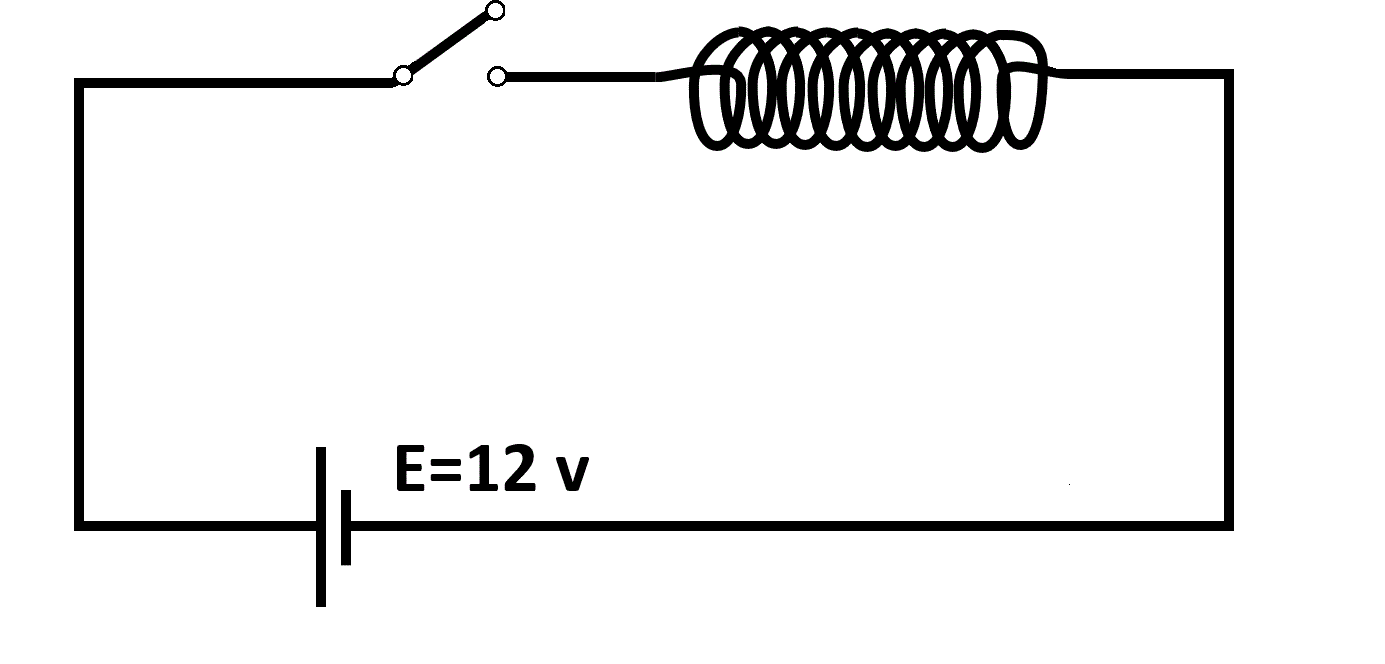
R: i(t) = 823,3 A/s t
Responder a
la pregunta b) del Problema 9.2- ( fuerza magnética ) y a
la pregunta c) del Problema 9.4-
utilizando la Regla de Lenz.