C O R R I E N T E A L T E R N A

PROBLEMA 12.1.–

En el circuito de la figura la tensión eficaz de la fuente es V_{f ef} = 60 V y su frecuencia es el doble de la frecuencia de resonancia del circuito.

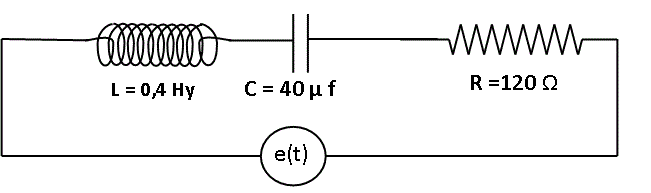
a) Expresar la tensión de la fuente en función del tiempo

b) Encontrar la expresion corriente en función del tiempo i(t)

c) Calcular potencia media disipada

d) Hacer el diagrama fasorial de impedancias.

R: a) V_f(t) = 84,85 V sen (500 1/s . t + 51,34^o) b) i(t) = 441,7 mA sen (500 1/s . t ) c) P = 11,4 W

PROBLEMA 12.2.–

El circuito de la figura disipa una potencia P = 800 W (potencia media). La corriente eficaz es Ief = 5 A.

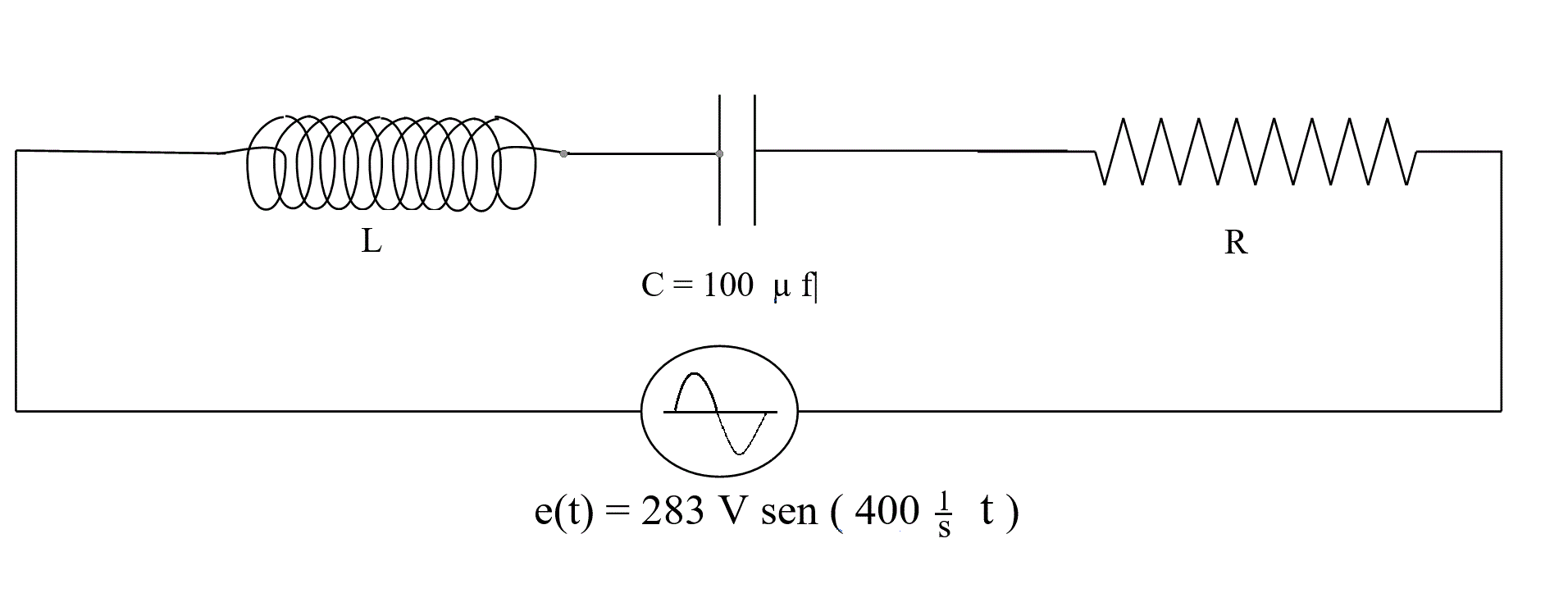
a) Calcular el valor de L.

b) Hacer el diagrama fasorial de impedancias.

R: a) Hay dos soluciones: 1) circuito inductivo: L = 0,1225 Hy = 122,5 mHy 2) circuito capacitivo: L= 0,0025 Hy = 2,5 mHy

PROBLEMA 12.3.–

En el circuito RL de la figura, conociendo el valor de la tension de la fuente y de la corriente en función del tiempo se pide hallar:

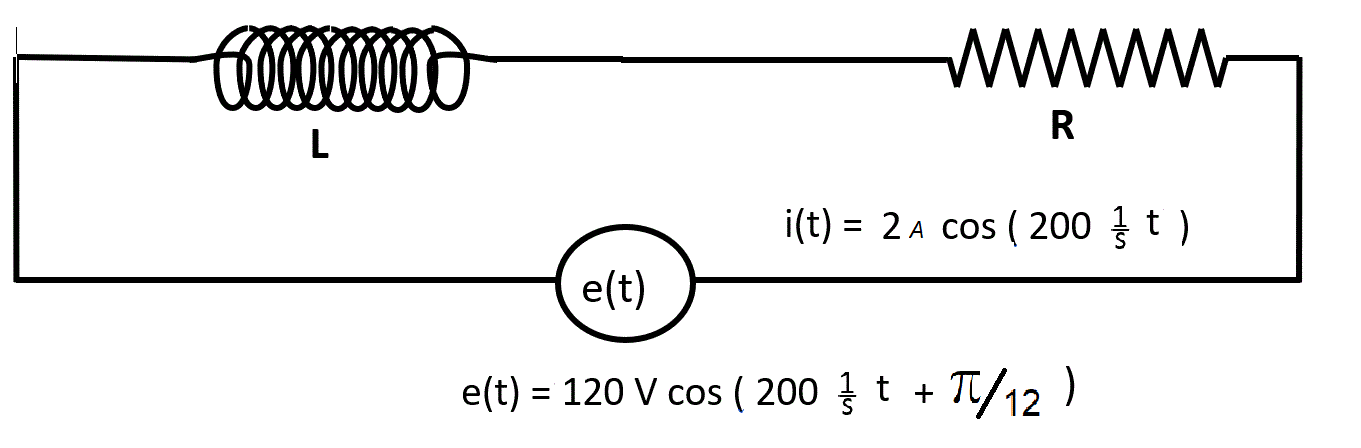
a) El valor de la resistencia R

b) El valor de la inductancia L
c) La potencia media disipada.

R: a) R = 57,95 Ω b) L = 77,64 mHy c) P = 115,91 W

PROBLEMA 12.4.–

Al aplicar una la tension e(t) = 160 V sen ( 400 1/s t ) al circuito RLC de la figura se verifica que este queda en resonancia. En ese momento, usando un voltímetro de valor eficaz, se mide la tension entre los puntos A y B y el instrumento indica 200 V .
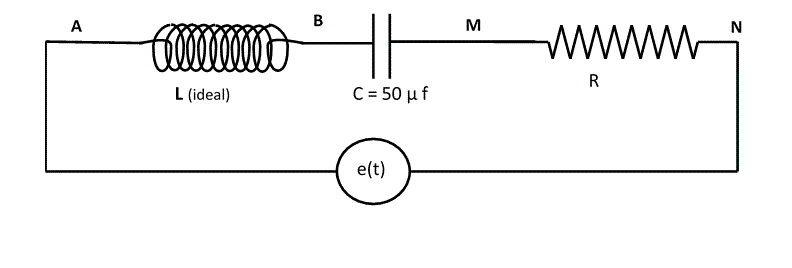
a) Hallar el valor de la resistencia R y de la inductancia L
b) Si luego la frecuencia de la tensión de la fuente se lleva al doble de su valor, se pide calcular el ángulo de fase y hacer el diagrma fasorial para esas condiciones.

R: a) R = 28,28 Ω L = 0,125 Hy b) φ = 1,21 rad. = 69,34 ^o

PROBLEMA 12.5.–

El circuito RLC de la figura está en resonancia. La tensión sobre los extremos de capacitor en función del tiempo es v_c(t) = 50 V . sen (400 1/s t – π/2 )
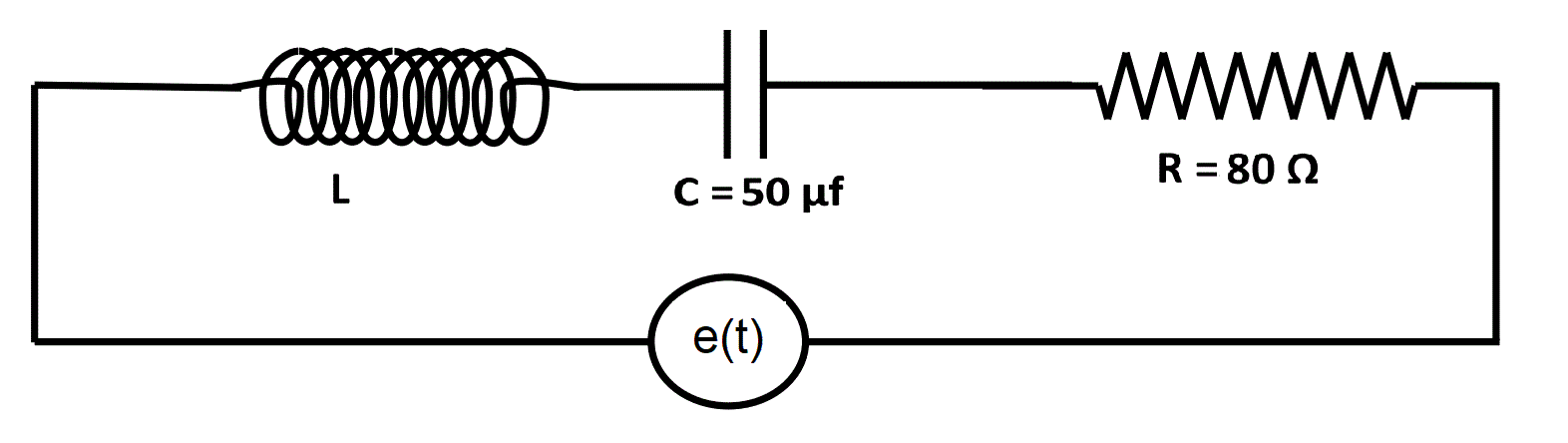
Calcular:
a) La tensión eficaz de la fuente.
b) La potencia disipada
c) Hacer el diagrama fasorial de tensiones.
d) Hacer el diagrama fasorial de impedancias.

R: a) V_eff = 56,56 V b) P= 40 W

PROBLEMA 12.6.–

El circuito RLC de la figura tensión de la fuente en función del tiempo es v_f(t) = 300 V . sen(250 1/s t – π/9)
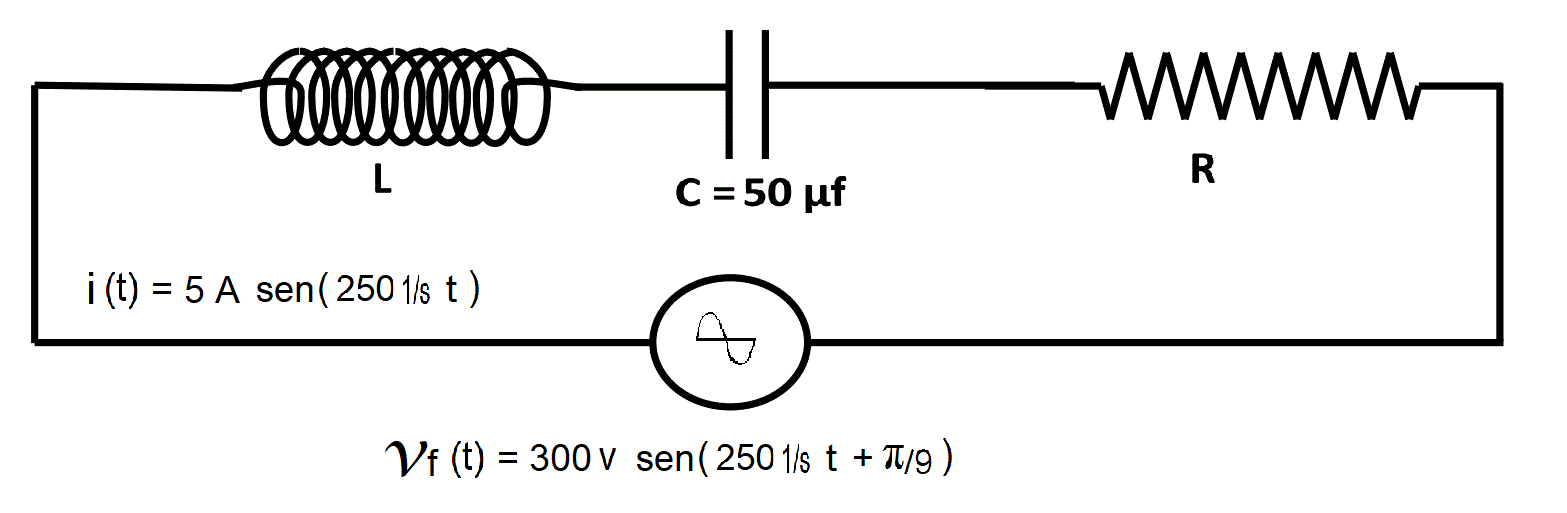
La corriente en función del tiempo vale i(t) = 5 A sen(250 1/s t).
Calcular:
a) La potencia disipada
b) El valor de la resistencia R
c) El valor de la inductancia ideal L

R: a) P = 1.409,54 W b) R = 56,38 Ω c) L = 0,238 Hy

VOLVER