|
Cuatro litros de gas ideal diatómico (cv = 5/2 R) que están una presión P = 400 KPa, se expanden de manera isotérmica reversible hasta duplicar su volumen: a → b Luego el gas se contráe a presión constante hasta el volumen inicial: b → c Finalmente se lo calienta a volumen constante hasta que alcanza la presión original: c → a a) Dibujar el ciclo en el diagrama P/V. b) Calcular el rendimiento del ciclo. c) ¿Cuál sería el rendimiento de una máquina de térmica de Carnot que operara entre las mismas temperaturas? |
|
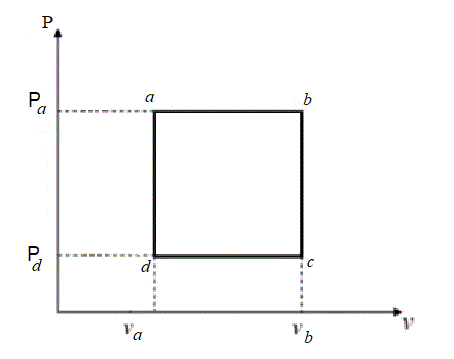
Dos moles de un gas ideal diatómico (cv=5/2R) describen un ciclo termodinámicos que está compuesto por cuatro trasformaciones: a→b isobárica, b→c isocórica, c→d isobárica y d→a isocórica. El trabajo en la trasformación c→d es Wcd = -3.600 J Datos: Número de moles n = 2 Va = 20 litros Vb = 40 litros Temperatura en el estado a: Ta = 673 K. Calcular a) El calor en cada una de las trasformaciones. b) El rendimiento η del ciclo. c) ¿Cuál seria el rendimiento de una máquina térmica de Carnot con las mismas temperaturas extremas de este ciclo? |
 |
|
Una máquina térmica trabaja entre dos fuentes cuyas temperaturas son a 100 K y 500 K. En cada ciclo absorbe 1000 J de calor del foco caliente. Su rendimiento es del 20%. a) Indicar si la máquina funciona reversible o irreversiblemente. Justificar b) Determinar la variación de entropía ΔS del universo en cada ciclo. c) Repetir el calculo anterior para una maquina de Carnot que utilice esas fuentes. |
| En un calorímetro ideal que contiene 900 g de agua a 27 ºC, se introducen 450 g de agua a 87 ºC. Calcular el aumento de entropía del universo. |