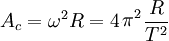Newton y la Luna . . . . . Dedicado a Lara |
"Yo me veo como un niño pequeño jugando en la playa que disfruta al encontrar, de cuando en cuando un guijarro más fino o una conchilla más bonita de lo común, mientras el gran océano del conocimiento se extiende ante él, inexplorado" Isaac Newton |
En 1666 Newton imaginó que la gravedad de la Tierra ejerce influencia sobre la Luna actuando como una "fuerza centrípeta". A partir de la cinematica del movimiento circular comenzó a vislumbrar lo que serían las leyes fundamentales de la mecánica celeste.
"En ausencia de fuerzas externas, un cuerpo en movimiento adopta una trayectoria rectilínea con movimiento uniforme"
Fue este el "primer principio" enunciado por Newton: el Principio de Inercia.
La Luna en su movimiento alrededor de la Tierra describe una trayectoria que no es recta. Newton sabía que, si el principio de inercia se cumple, incluso en la Luna, debía entonces existir una fuerza. Pero ... ¿ qué tipo de fuerza ?
Desde el punto de de vista de la Cinemática, es decir de la descripción del movimiento, se trata de una:
"fuerza centrípeta"
Centrípeta: del latín "centrum" : centro , "petere" : tender a : dirigida al centro, en este caso al centro de la Tierra.
Del estudio del movimiento circular surge el valor de la aceleración centrípeta:
| R = Radio del movimiento | T = Período | 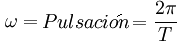 |
Fue en 1673 que Huygen's publicó por primera vez esta fórmula.
De acuerdo al Segundo Principio o Principio de Masa la fuerza es el producto de la masa por la aceleración. La fuerza centrípeta será entonces el producto de la masa por la aceleración centrípeta. En el caso del movimiento de la Luna alrededor de la Tierra la fuerza centrípeta está dirigida hacia el centro de la Tierra. El peso de los cuerpos y la aceleración de la gravedad aquí en la Tierra - el vector g !! - tiene siempre dirección "hacia abajo", concepto local que significa: con dirección al centro del Planeta .
Newton postuló : es posible que la fuerza peso que "se manifiesta aún en las más altas montañas se extienda hasta alturas impensadas llegando, por qué no hasta la Luna, influenciando su movimiento, siendo quizás la causa que la retiene en su órbita".
Esta parecía ser una hipótesis digna de atención . . . pero la aceleración de la Luna y de un cuerpo aquí en la Tierra resultaron tener valores muy distintos.
Los valores del movimiento de la Luna alrededor de la Tierra, son :
Período = T = 27,3 días x ( 24 horas / día) x ( 3600 s /hora) = 2.358.720 segundos
Radio de la órbita lunar = R = 384.000 Km.
Con estos valores obtenemos una aceleración :
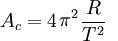
AC =39,47 x 384.000.000 m /(2.358.720 s)2
AC = 0,002725 m/s2
peso de los cuerpos en la Tierra produce sobre ellos una aceleración de 9,82 m/s2. (Módulo del vector g). El valor calculado para la Luna : 0.00275 m/s2 es mucho menor. ¿En qué proporción ? La relación es :
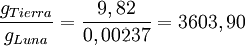
Aproximadamente 3600. Con poco margen de error podemos decir que la gravedad es 3600 veces menor en la Luna con respecto a su valor en la superficie de la Tierra.
VARIACIÓN CON LA DISTANCIA
Newton sabía que la distancia media Tierra-Luna ronda los 384.000 Km.
El radio de la Tierra se acerca a los 6.400 Km.
Si dividimos
384.000 Km / 6.400 Km = 60
Entonces la distancia Tierra-Luna equivale a 60 radios terrestres.
Elevando al cuadrado es:
602 = 3600
Estos cálculos le hicieron pensar en una fuerza de gravedad inversamente proporcional al cuadrado de la distancia. No obstante esta era solo una hipótesis de trabajo. Para que esa hipótesis diera sus frutos, un largo camino quedaba aún por recorrer. Las leyes de Kepler y el flamante calculo de fluxiones inversas serían fundamentales en ese proceso.
RELACIÓN CON LA MASA
Hagamos un experimento terrestre: dejemos caer una manzana.
De acuerdo al principio de masa es:
F = P = m . g
Experimentalmente se puede comprobar que la aceleración de un cuerpo en caída libre en el vacío, el vector g , es independiente de su masa. Al ser g constante la fuerza de gravedad resulta, en consecuencia, proporcional a la masa m del cuerpo (manzana) que es atraído hacia la Tierra. Ahora bien, de acuerdo al principio de acción y reacción la Tierra recibe de este cuerpo una fuerza de igual dirección y módulo y sentido contrario. Si la materia atrae a la materia, la manzana atrae a la Tierra tal como la Tierra atrae a la manzana. Es decir el cuerpo que genera la atracción es también un cuerpo atraído. La fuerza F sigue siendo proporcional a la masa pero ahora que se trata de la fuerza de que ejerce la manzana sobre la Tierra y será proporcional a la masa del planeta.
"Si la masa atrae la masa, esto debe ocurrir proporcionalmente a su cantidad"
Con validez, tanto en referencia a la masa de la manzana como para la masa de la Tierra. Newton postuló:
"Existe una fuerza de gravedad, que se extiende por todo el
universo, por la cual cada porción de materia atrae a toda otra porción de materia en proporción directa al producto de las masas y en proporcion inversa al cuadrado de la distancia "
El problema del campo de la esfera
Para objetos cuyas dimensiones son pequeñas en relación a las distancias que los separan, no hay demasiados conflictos al hablar de distancias pero para un objeto cercano a la Tierra la fuerza total resulta de aplicar el principio de superposición para la atracción que ejerce sobre él cada partícula de materia del planeta. Si lo consideramos como una esfera homogénea o de densidad solo dependiente del radio, la fuerza resultante es la que existiría si toda la masa estuviera concertada en el centro. A Newton el problema lo preocupó por años. Debió convencerse y luego probar la validez esta equivalencia. En 1686 escribe en una carta al astrónomo Edmund Halley:
"Es una objecion tan importante que sin la demostracion que he hecho de esta equivalencia un filosofo sensato no podria creer que mi teoria sea ni cercanamete correcta "
En 1687 Newton, alentado por Haley, finalmente publica "Philosophiae Naturalis Principia Mathematica" ("Principios matemáticos de la Filosofía Natural") donde expone la Teoría de la Gravitación. Es interesante observar que en las demostraciones, Newton no hace referencia expresa al calculo de fluxiones que él venía desarrollando desde 1660. Más bien prefiere las demostraciones de tipo geométrico, tal como los antiguos, al estilo de Euclides o Arquímedes. No obstante el Cálculo es el fundamento implícito de los desarrollos de Principia.
He incluído algunas demostraciones de ambos tipos en los links que siguen: