Campo de una esfera

Campo gravitatorio de una esfera homogénea

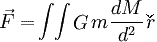
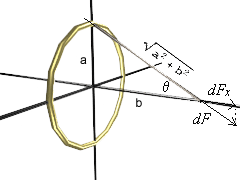
Para una esfera de radio R imaginemos sobre su superficie una concentración de masa en una capa de pequeño espesor. La densidad superficial σ, esto es la masa por unidad de superficie, es constante. Notemos que G σ tiene las dimensiones de una aceleración. A una distancia d del centro de la esfera, con d > R hay un cuerpo de masa m y dimensiones que consideradas despreciables con respecto al las de la esfera, por ejemplo ... nuestra manzana. La fuerza de atracción es:

La aceleración de la manzana esta dada por cociente

Es el campo gravitatorio o vector g.
La integración se puede realizar de distintas maneras según las variables o coordenadas o que se utilicen para recorrer la superficie. El eje que une los centros de ambos cuerpos es eje de simetría. Podemos tomar ese eje como eje x, con origen en el centro O de la superficie esférica. Los distintos valores de x determinan planos normales al eje. La porción de la superficie de la esfera comprendica entre dos planos paralelos es una zona esférica

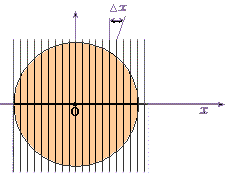
Su área es igual a la de la superficie lateral de la porción del cilindro inscripto en la esfera que está comprendida entre ambos planos. Fue Arquímedes quien encontró esta propiedad utilizando el método denominado de exhaustión, precedente del cálculo integral.

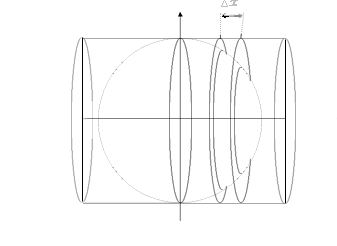
Para zona esférica comprendida entre los planos x = xo y x = xo + Δx con -R < x < R, el área resulta:

ΔA = 2 π R Δx

y su diferencial es :

dA = 2 π R dx

Es interesante notar que el valor de esta área diferencial es independiente de x.

Otra forma de ver este resultado es la siguiente:

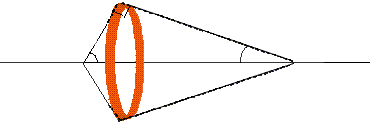
Para Δx pequeño el perímetro del anillo tiende a: p = 2 π R . sen θ

La longitud del arco se aproxima con: Δs = Δx / cos φ = Δx / sen θ

El área es el producto: ΔA = p Δs = 2 π r sen θ . Δx/sen θ = 2 π R Δx

En el límite es: dA = 2 π R dx

Para obtener el diferencial de masa multiplicamos el diferencial de área por la densidad superficial σ:

dM = σ dA

dM = 2 π σ R dx

CAMPO DE UN ANILLO

En este caso la la distancia y el ángulo con el eje no varian para los distintos elementos de masa del anillo.
El campo gravitatorio a una distancia b del centro de un anillo o espira de radio a y masa dM vale

En este caso la distancia al centro del anillo es b = d - x y para el radio del anillo es a² = R²- x². Entonces

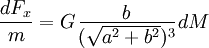
Si reemplazamos dM por 2 π σ R dx obtenemos:

La integral indefinida vale

Al poner los límites -R y R resulta

Si R > d es igual a 0. Efectivamente, el campo gravitacional en el interior de una esfera homogénea hueca es nulo.
Si R < d la integral definida es igual a

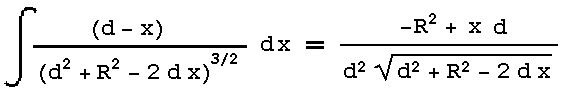
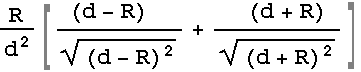
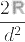. Reemplazando resulta:

Pero 4 π R² es el área total de la esfera. Multiplicada por la densidad superficial σ nos da la masa total M.
El valor entonces resulta:

Es por lo tanto correcto, en lo que a fuerzas externas se refiere, suponer toda la masa M concentrada en el centro.
Este resultado se extiende, por superposición, a una esfera maciza en la que la densidad es función sólo del radio.